微积分的基础知识与应用

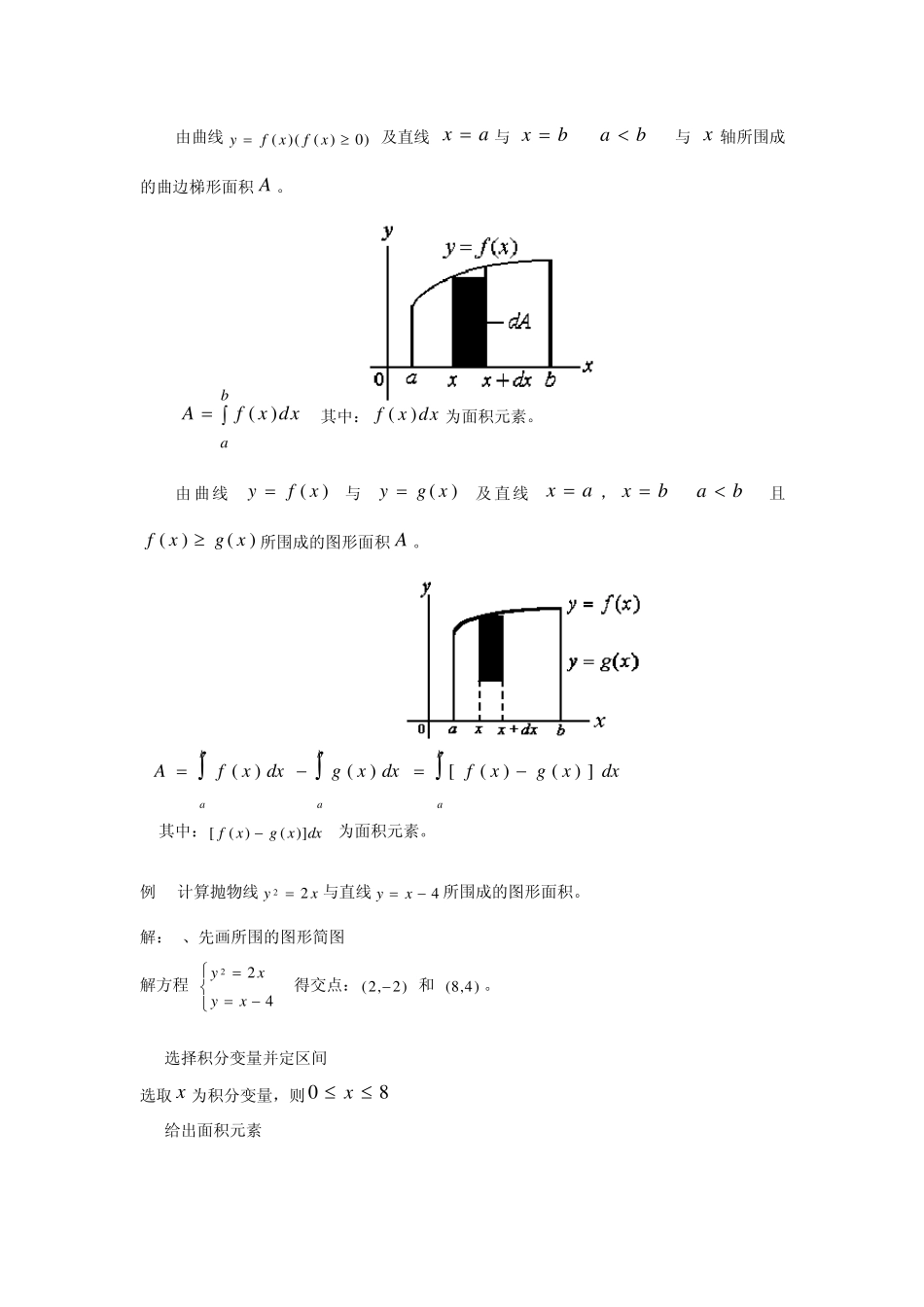
微积分的基础知识 微分中的u ,d ,v 是什么意思？ u、v 是用来代表函数的，例如u=f(x)，v=g(x)等， 这样写其公式来比较简洁， 而且选择u、v 不会那么容易造成混淆； d 是微分符号，如dx 表示x 的微分，相当于极微小的一部分x， 这也是微分的叫法； 相应的，∫表示积分， 例如∫udx 即相对于函数u 的很多微分dx 累积在一起的和。 微元法 1．能用定积分计算的量U ，应满足下列三个条件 (1) U 与变量 x 的变化区间],[ba有关； (2) U 对于区间],[ba具有可加性； (3) U 部分量iU可近似地表示成iixf)(。 2．写出计算U 的定积分表达式步骤 (1) 根据问题，选取一个变量 x 为积分变量，并确定它的变化区间[,]a b ； (2) 设想将区间[ , ]a b 分成若干小区间，取其中的任一小区间[ ,]x xdx， 求出它所对应的部分量 U 的近似值 dxxfU)( ( fx() 为[,]a b 上一连续函数) 则称 fxdx()为量U 的元素，且记作dxxfdU)(。 (3) 以U 的元素 dU 作被积表达式，以[,]a b 为积分区间，得 badxxfU)( 这个方法叫做微元法，其实质是找出U 的元素 dU 的微分表达式 )()(bxadxxfdU. 二、平面区域的面积 1、直角坐标的情形 由曲线)0)(()(xfxfy 及直线 xa与 xb ( ab ) 与 x 轴所围成的曲边梯形面积A 。 Afx dxab () 其中：fx dx()为面积元素。 由曲线 yfx() 与 yg x() 及直线 xa，xb( ab )且fxg x()()所围成的图形面积A 。 bababadxxgxfdxxgdxxfA])()([)()( 其中：dxxgxf])()([ 为面积元素。 例1 计算抛物线 xy22 与直线 4 xy所围成的图形面积。 解：1、先画所围的图形简图 解方程 422xyxy, 得交点：)2,2( 和 )4,8(。 2. 选择积分变量并定区间 选取 x 为积分变量，则08x 3. 给出面积元素 在 20 x上， dxxdxxxdA22])2(2[ 在82 x上， dxxxdxxxdA)24(])4(2[ 4. 列定积分表达式 18213224324]24[228222320238220xxxxdxxxdxxA 另解：若选取y 为积分变量，则 42y dyyydA]21)4([2 18642)214(4232242yyydyyyA 显然，解法二较简洁，这表明积分变量的选取有个合理性的问题。 2、极坐标情形 设平面图形是由曲线 )(r及射线 ，...