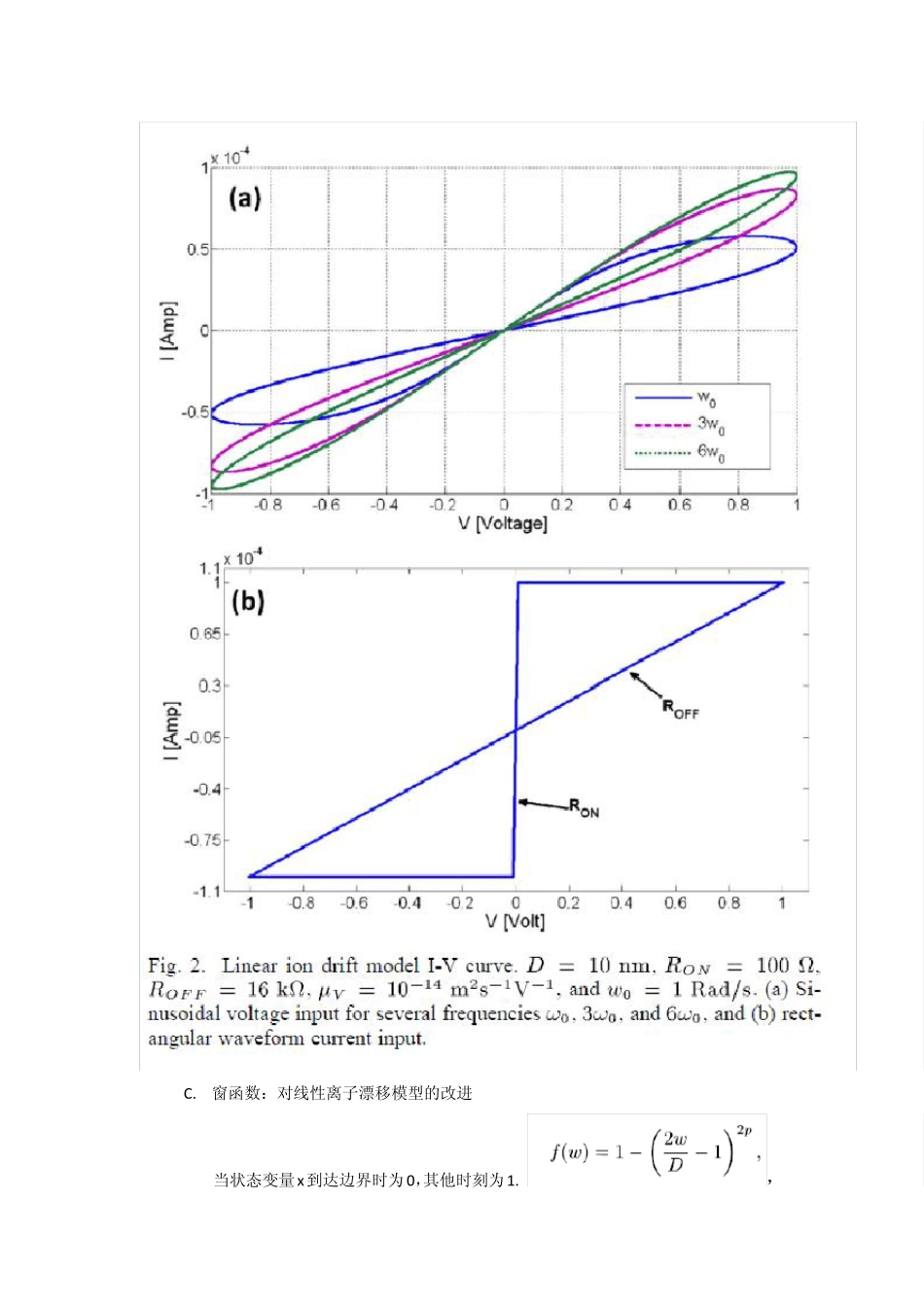
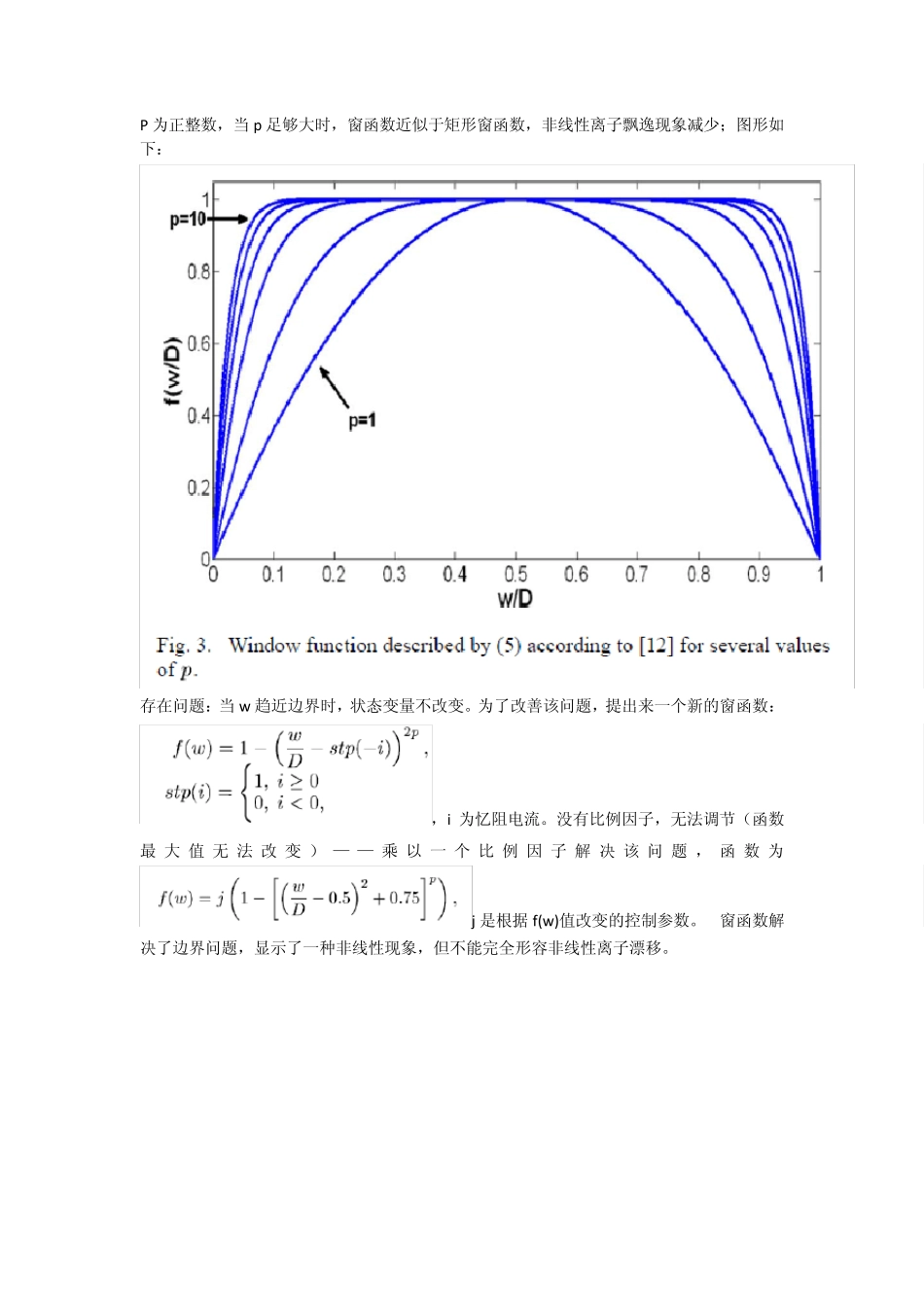
TEAM: ThrEshold Adaptiv e Memristor Model 1. 介绍 2. 对忆阻装置特征的需求:随内部状态改变的阻值;非易失性;内部状态依赖于电荷的非线性,电流越高改变越大(保证无损的读取机制); 3. 如今提出的忆阻模型: A. 基本需求:精确,计算效率,模型简单直观,封闭式的;普遍适用 B. 线性离子漂移模型 C. 窗函数:对线性离子漂移模型的改进 当状态变量x到达边界时为0,其他时刻为1. ,P 为正整数,当p 足够大时,窗函数近似于矩形窗函数,非线性离子飘逸现象减少;图形如下: 存在问题:当w 趋近边界时,状态变量不改变。为了改善该问题,提出来一个新的窗函数:,i 为忆阻电流。没有比例因子,无法调节(函数最大值无法改变)— — 乘 以 一个比例因子解 决 该问题,函数为j 是根据 f(w )值改变的控制参数。 窗函数解决了边界问题,显示了一种非线性现象,但不能完全形容非线性离子漂移。 未加比例因子;改进后。 D. 非线性离子漂移模型 逻辑电路需要更多的非线性I-V特性,(参考文献 15),该模 型 假 设 了 一 种 不 对 称 的 转 换 关 系 , 状 态 变 量 对 电 压 的 非 线 性 依 赖a.m 常数,m 奇整数,f(w )窗函数。 E. Simmons 隧道结模型 假 设 非 线 性 与 不 对 称 性 来 源 于 电 离 子 掺 杂 物 的 运 动 的 指 数依 赖 。,表示氧空位的迁移速度。正向电压,co ff 更大,氧空位迁移更快。 4 . 自适应阈值忆阻模型 V-I 关系未确定,能适用于各种情况。A:前文提到的模型缺陷及对现提出模型的需求;B,C:描述状态变量导数,I-V 关系。D:适当的窗函数。 A. 对简化模型的需求 首先,simmons 模型十分精确,但很复杂并且只适用于特定的忆阻器(论文 21 提出 SPICE 仿真);计算不效率。简化模型要求计算简单,方程式更加简化,而需要足够的精确度。假定阈值以下 X 不会变化,依赖于多项式而非指数。 B. TEAM 模型的状态变量导数 C. TEAM 模型 V-I 关系 根据HP模型,由隧道结模型联系到阻值改变的指数性规则: D. 将隧道结模型适用于TEAM 模型 由于模拟引擎的离散性质,边界可超过,下图分别是理想窗函数与假定窗函数,后者将状态变量控制在一个更小的范围,忆阻激活时间更快 5 . 两种模型之间的比较 表1:不同忆阻器比较;表2,不同窗函数比较 通过设定参数值,该模型能转换为不同的忆阻器模型,