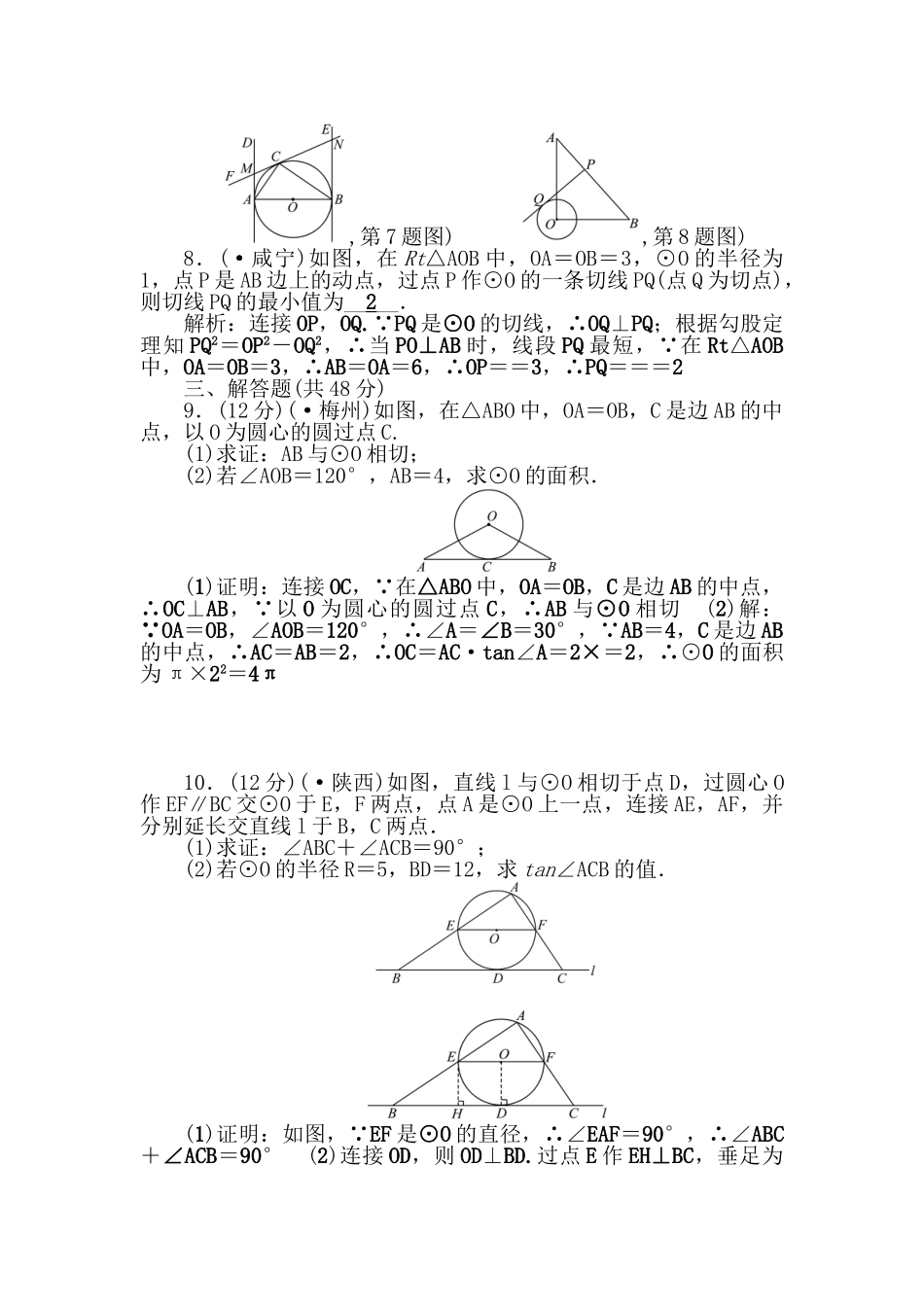
直线与圆的位置关系一、选择题(每题 6 分,共 24 分)1.(·白银)已知⊙O 的半径是 6 cm,点 O 到同一平面内直线 l的距离为 5 cm,则直线 l 与⊙O 的位置关系是( A )A.相交 B.相切C.相离 D.无法判断2.(·黔东南州)Rt△ABC 中,∠C=90°,AC=3 cm,BC=4 cm,以 C 为圆心,r 为半径作圆,若圆 C 与直线 AB 相切,则 r 的值为( B )A.2 cm B.2.4 cm C.3 cm D.4 cm3.(·邵阳)如图,△ABC 的边 AC 与⊙O 相交于 C,D 两点,且通过圆心 O,边 AB 与⊙O 相切,切点为点 B.已知∠A=30°,则∠C的大小是( A )A.30° B.45° C.60° D.40°4.(·内江)如图,Rt△ABC 中,∠ACB=90°,AC=4,BC=6,以斜边 AB 上的一点 O 为圆心所作的半圆分别与 AC,BC 相切于点D,E,则 AD 为( B )A.2.5 B.1.6 C.1.5 D.1解析:连接 OD,OE,设 AD=x, 半圆分别与 AC,BC 相切,∴∠CDO=∠CEO=90°, ∠C=90°,∴四边形 ODCE 是矩形,∴OD=CE,OE=CD,∴CD=CE=4-x,BE=6-(4-x)=x+2, ∠AOD+ ∠ A = 90° , ∠ AOD + ∠ BOE = 90° , ∴ ∠ A =∠BOE,∴△AOD∽△OBE,∴=,∴=,解得 x=1.6,故选 B二、填空题(每题 7 分,共 28 分)5.(·湘潭)如图,⊙O 的半径为 3,P 是 CB 延长线上一点,PO=5,PA 切⊙O 于 A 点,则 PA=__4__.,第 5 题图) ,第 6 题图)6.(·天津)如图,PA,PB 分别切⊙O 于点 A,B,若∠P=70°,则∠C 的大小为__55 ° __.7.(·宜宾)如图,已知 AB 为⊙O 的直径,AB=2,AD 和 BE 是圆 O 的两条切线,A,B 为切点,过圆上一点 C 作⊙O 的切线 CF,分别交 AD,BE 于点 M,N,连接 AC,CB,若∠ABC=30°,则 AM=____.,第 7 题图) ,第 8 题图)8.(·咸宁)如图,在 Rt△AOB 中,OA=OB=3,⊙O 的半径为1,点 P 是 AB 边上的动点,过点 P 作⊙O 的一条切线 PQ(点 Q 为切点),则切线 PQ 的最小值为__2__.解析:连接 OP,OQ. PQ 是⊙O 的切线,∴OQ⊥PQ;根据勾股定理知 PQ2=OP2-OQ2,∴当 PO⊥AB 时,线段 PQ 最短, 在 Rt△AOB中,OA=OB=3,∴AB=OA=6,∴OP==3,∴PQ===2三、解答题(共 48 分)9.(12 分)(·梅州)如图,在△ABO 中,OA=OB,C 是边 AB 的中点,以 O 为圆心的圆过点 C.(1)求证:A...