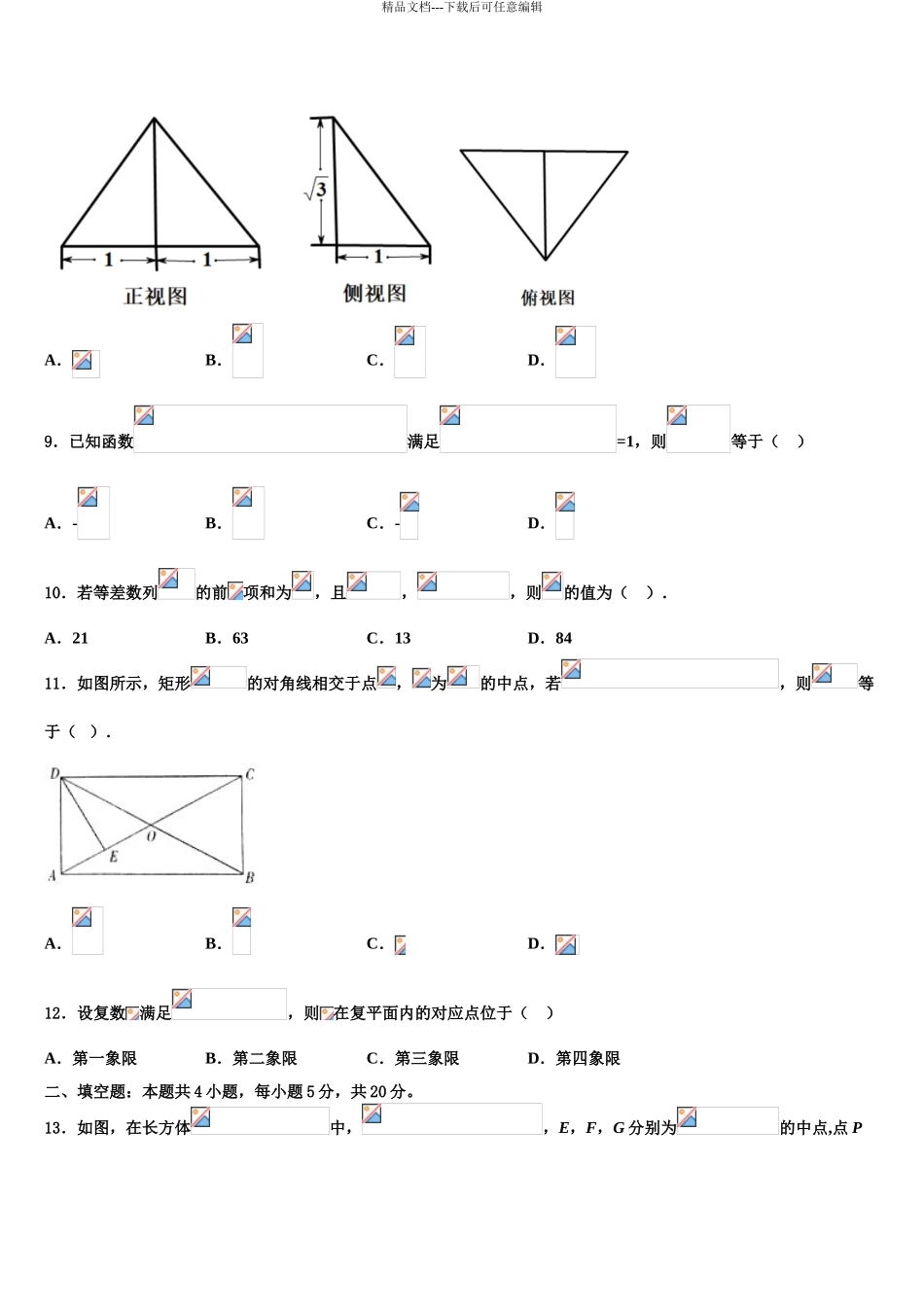
精品文档---下载后可任意编辑2024-2024 高考数学模拟试卷含解析考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的洁净。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.如图,在中,点是的中点,过点的直线分别交直线,于不同的两点,若,,则( )A.1B.C.2D.32.《九章算术》勾股章有一“引葭赴岸”问题“今有饼池径丈,葭生其中,出水两尺,引葭赴岸,适与岸齐,问水深,葭各几何?”,其意思是:有一个直径为一丈的圆柱形水池,池中心生有一颗类似芦苇的植物,露出水面两尺,若把它引向岸边,正好与岸边齐,问水有多深,该植物有多高?其中一丈等于十尺,如图若从该葭上随机取一点,则该点取自水下的概率为( )A.B.C.D.3.若集合,,则下列结论正确的是( )A.B.C.D.4.设等差数列的前项和为,若,则( )A.10B.9C.8D.75.在中,内角 A,B,C 所对的边分别为 a,b,c,且.若,的面积为,则( )A.5B.C.4D.166.若函数的图象上两点,关于直线的对称点在的图象上,则的取值范围是( )A.B.C.D.7.明代数学家程大位(1533~1606 年),有感于当时筹算方法的不便,用其毕生心血写出《算法统宗》,可谓集成计算的鼻祖.如图所示的程序框图的算法思路源于其著作中的“李白沽酒”问题.执行该程序框图,若输出的的值为,则输入的的值为( )A.B.C.D.8.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积为( )精品文档---下载后可任意编辑 A.B.C.D.9.已知函数满足=1,则等于( )A.-B.C.-D.10.若等差数列的前项和为,且,,则的值为( ).A.21B.63C.13D.8411.如图所示,矩形的对角线相交于点,为的中点,若,则等于( ).A.B.C.D.12.设复数满足,则在复平面内的对应点位于( )A.第一象限B.第二象限C.第三象限D.第四象限二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.如图,在长方体中,,E,F,G 分别为的中点,点 P在平面 ABCD 内,若直线平面 EFG,则线段长度的最小值是________________.14.已知,满足约...