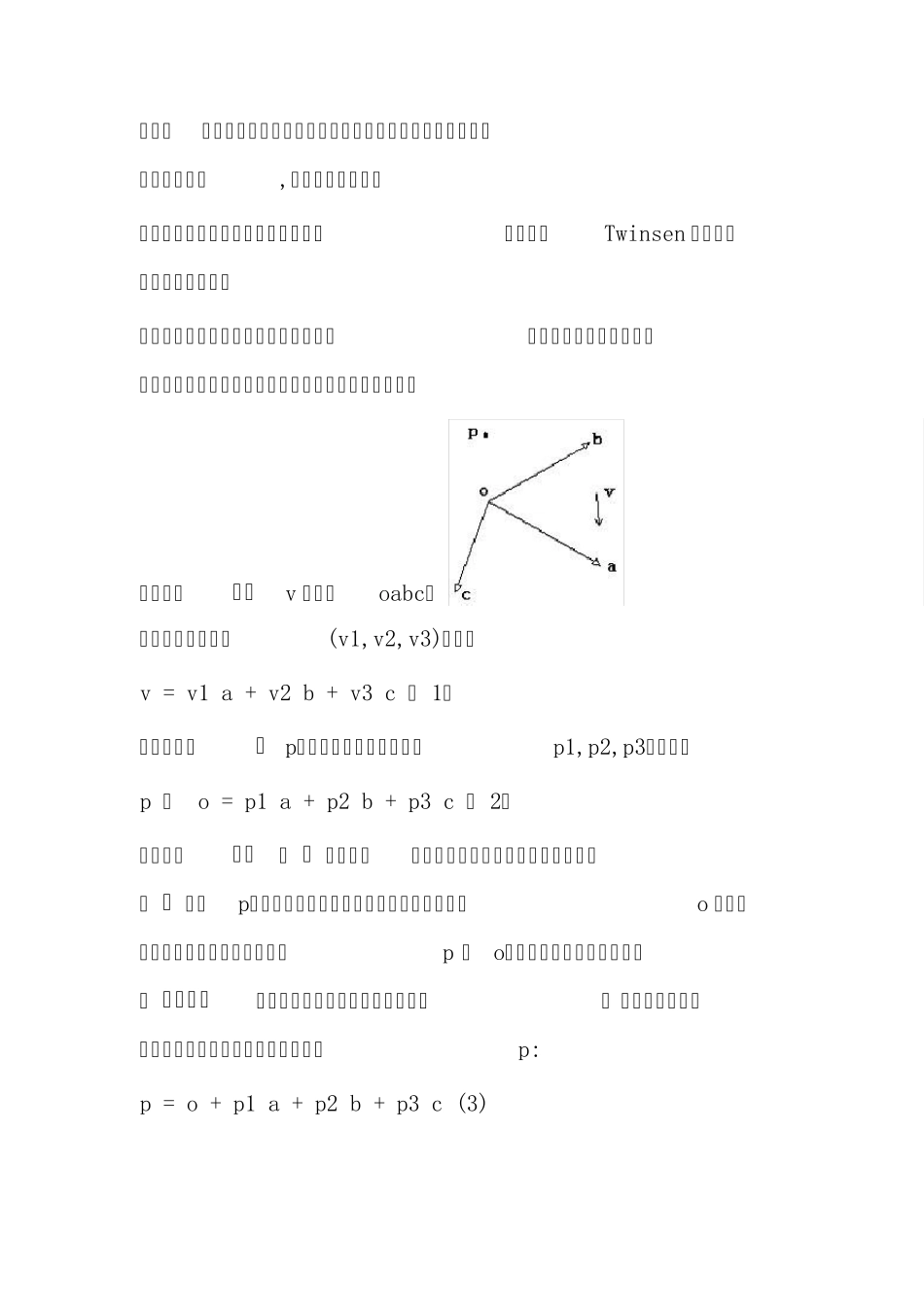
投 影 矩 阵 的 推 导 (OpenGL D3D) OpenGL 矩阵推导——模型视图变化 在三维编程中,模型视图变换是从三维世界到二维屏幕中一个很重要的变换,但是这个变换往往很多人都不太理解,要么是事而非。 而这方面的文章不是太少就是讲的太浅没有真正的理解模型视图变换,本人在这个过程中曾经走过很多歪路,不过好在最终在自己的不懈努力下终于降伏了这只猛虎。本人就以自己的理解,通过矩阵推导过程一步一步来了解模型视图变化,最后通过两个OpenGl 的程序来进一步理解模型视图矩阵。先从一个基本的模型视图—透视投影变换讲起。 透射投影是将相机空间中的点从视锥体(frustum)变换到规则观察体(Canonical View Volume 以下简称CVV)中,待裁剪完毕后进行透视除法的行为。 透视投影变换是令很多刚刚进入3D 图形领域的开发人员感到迷惑乃至神秘的一个图形技术。其中的理解困难在于步骤繁琐,对一些基础知识过分依赖,一旦对它们中的任何地方感到陌生,立刻导致理解停止不前。 主流的3D APIs 都把透射投影的具体细节进行了封装,从而只需一个函数便可生成一个透射投影矩阵比如gluPerspective(),使得我们不需要了解其算法便可实现三维到二维的转化,然而实事是,一些三维图形或游戏开发人员遇到一些视图矩阵的问题往往会不知所措,比如视景体裁剪。 以下部分内容是从别处那转过来的,主要感谢Twinsen 和一个叫丁欧南的高中生。 透视投影变换是在齐次坐标下进行的,而齐次坐标本身就是一个令人迷惑的概念,这里我们先把它理解清楚。齐次坐标 对于一个向量v 以及基oabc, 可以找到一组坐标(v1,v2,v3),使得 v = v1 a + v2 b + v3 c ( 1) 而对于一个点 p,则可以找到一组坐标(p1,p2,p3),使得 p – o = p1 a + p2 b + p3 c ( 2) 从上面对向量和 点 的表达,我们可以看出为了在坐标系中表示一个 点 (如p),我们把点的位置看作是对这个基的原点o 所进行的一个位移,即一个向量——p – o(有的书中把这样的向量叫做 位置向量——起始于坐标原点的特殊向量), 我们在表达这个向量的同时用等价的方式表达出了点p: p = o + p1 a + p2 b + p3 c (3) (1)(3)是坐标系下表达一个向量和 点 的不同表达方式。这里可以看出,虽然都是用代数分量的形式表达向量和点,但表达一个点比一个向量需要额外的信息。如果我写出一个代数分量表达(1, 4, 7),谁知道它是个向量还是个点...