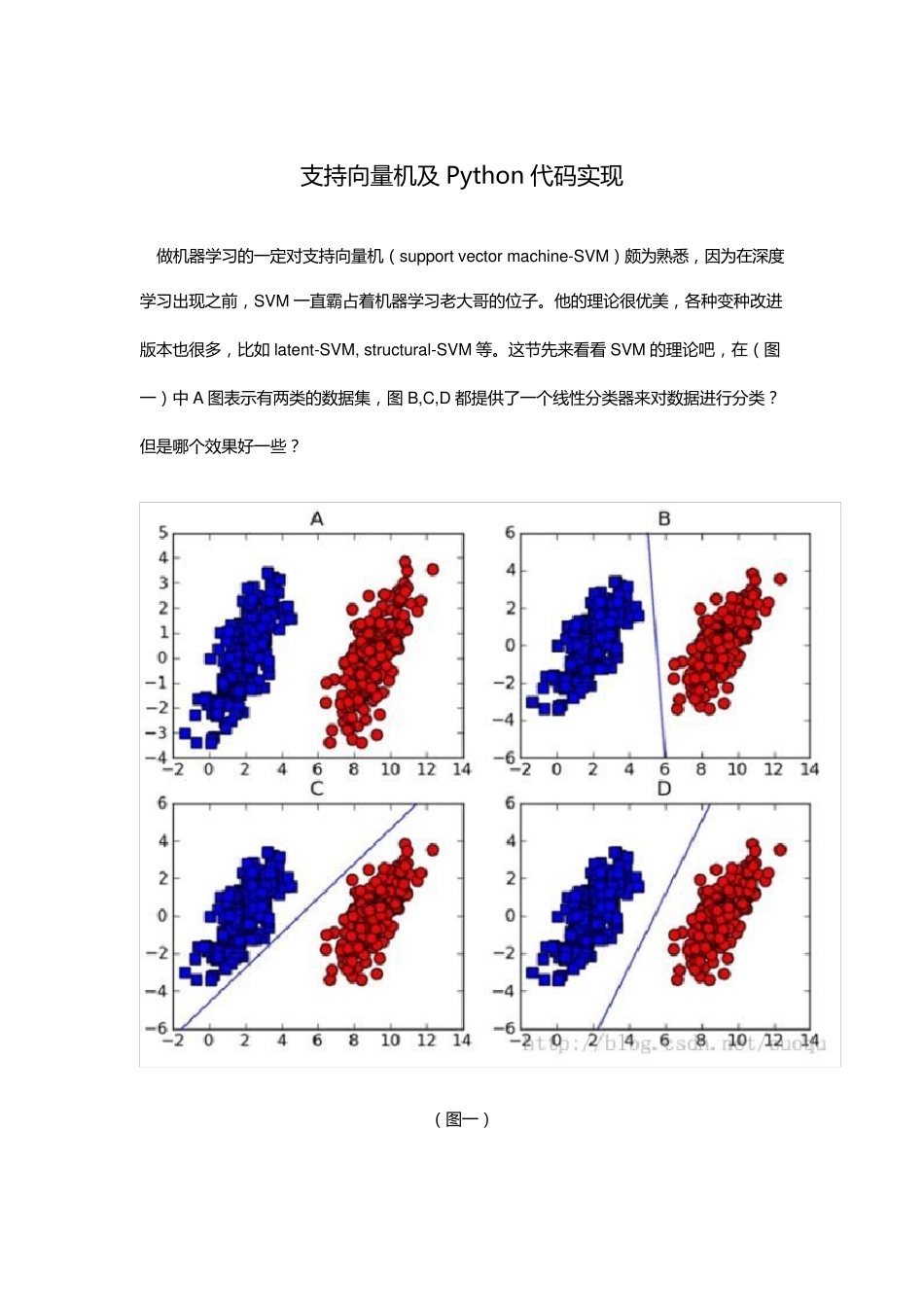
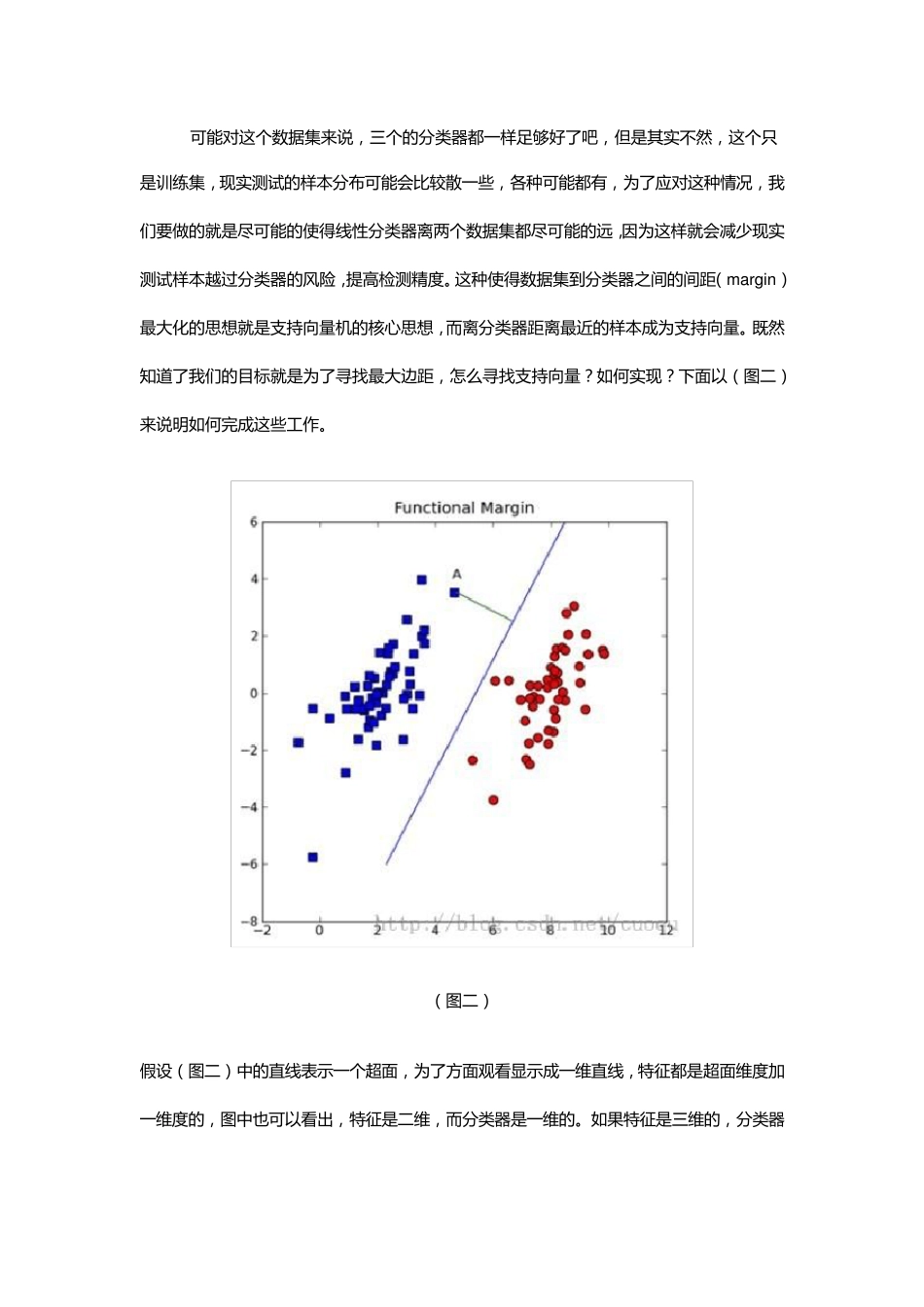
支 持 向 量 机 及 Python 代 码 实 现 做 机 器 学 习 的 一 定 对 支 持 向 量 机 ( support vector machine-SVM) 颇 为 熟 悉 , 因 为 在 深 度学 习 出 现 之 前 , SVM 一 直 霸 占 着 机 器 学 习 老 大 哥 的 位 子 。他的 理论很优美, 各种变种改进版本也很多, 比如 latent-SVM, structural-SVM 等。这节先来看看 SVM 的 理论吧, 在 ( 图一 ) 中 A 图表示有两类的 数据集, 图 B,C,D 都提供了一 个线性分类器 来对 数据进行分类?但是哪个效果好一 些? ( 图一 ) 可 能 对 这 个 数 据 集 来 说 , 三 个 的 分 类 器 都 一 样 足 够 好 了 吧 , 但 是 其 实 不 然 , 这 个 只是 训 练 集 , 现 实 测 试 的 样 本 分 布 可 能 会 比 较 散 一 些 , 各 种 可 能 都 有 , 为 了 应 对 这 种 情 况 , 我们 要 做 的 就 是 尽 可 能 的 使 得 线 性 分 类 器 离 两 个 数 据 集 都 尽 可 能 的 远 ,因 为 这 样 就 会 减 少 现 实测 试 样 本 越 过 分 类 器 的 风 险 , 提 高 检 测 精 度 。这 种 使 得 数 据 集 到分 类 器 之间的 间距(margin)最大化的 思想就 是 支持向量机的 核心思想, 而离 分 类 器 距离 最近的 样 本 成为 支持向量。既然知道了 我 们 的 目标就 是 为 了 寻找最大边距, 怎么寻找支持向量?如何实 现 ?下面以(图二)来 说 明如何完成这 些 工作。 (图二) 假设(图二)中的 直线 表示一 个 超面, 为 了 方面观看显示成一 维直线 , 特征都 是 超面维度 加一 维度 的 , 图中也可 以看出, 特征是 二维, 而分 类 器 是 一 维的 。如果特征是 三 维的 , 分 类 器就 是 一 个 平 面 。假设超面 的解析式为,那么点 A 到超面 的距离为,下面 给出这个 距离证明: (图三) 在(图三)中,青色菱形表示超面 ,Xn 为数据集中一 点,W 是 超面 权重,而且 W 是 垂直于超面 的。证明垂直很简单,假设 X’和 X’’都是 超面 上的一 点, ,因此 W 垂直于超面 。知道了 W 垂直于超面 ,那么 Xn 到超面 的距离其实就 是 Xn 和超面 上任意...