材料力学作业参考解答

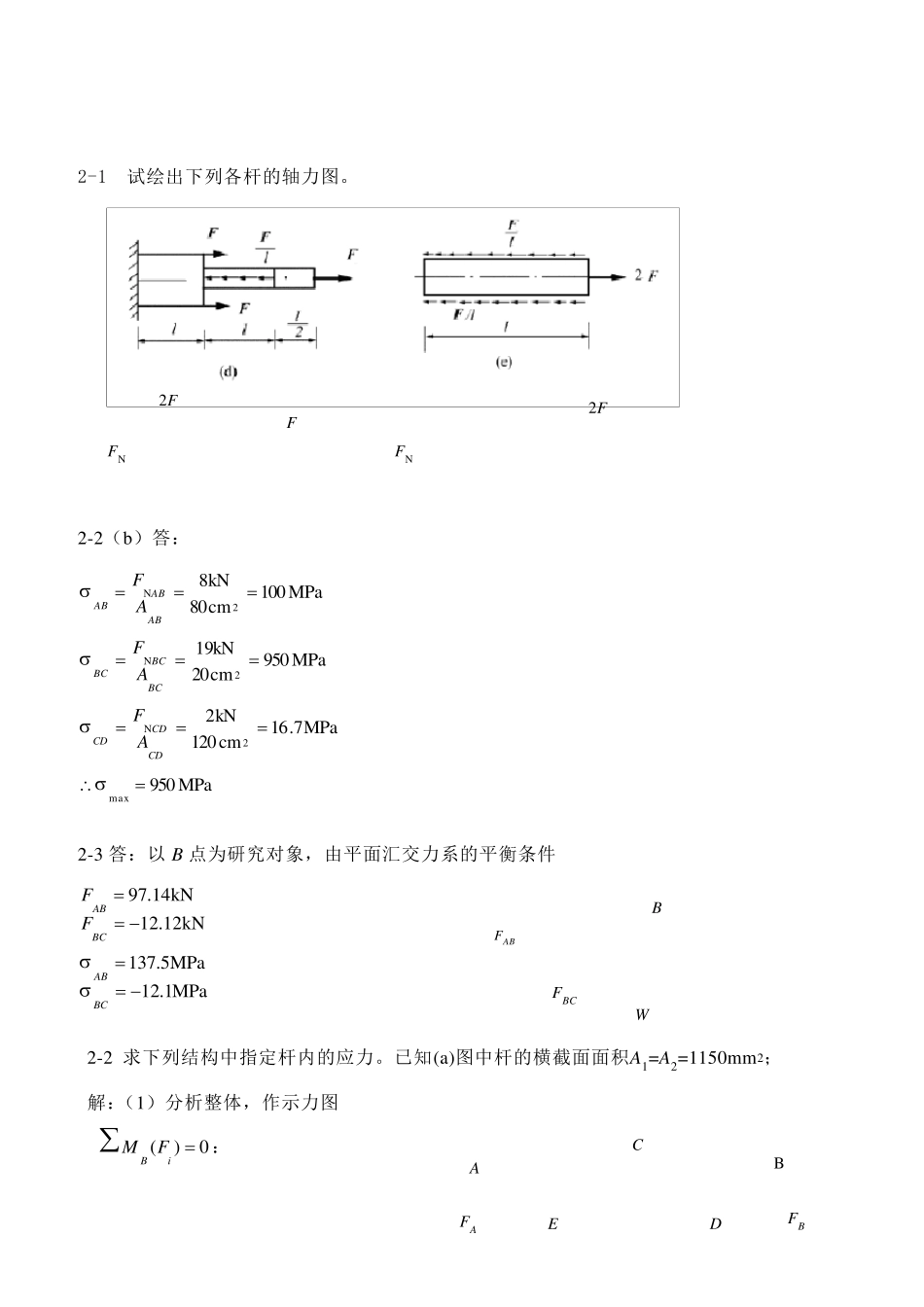
2-1 试绘出下列各杆的轴力图。 2-2（b）答： MPa100cm80kN82NABABABAF MPa950cm209kN12NBCBCBCAF MPa7.16cm120kN22NCDCDCDAF MPa950max  2-3 答：以 B 点为研究对象，由平面汇交力系的平衡条件 kN12.12kN14.97BCABFF MPa1.12MPa5.137BCAB 2-2 求下列结构中指定杆内的应力。已知(a)图中杆的横截面面积A1=A2=1150mm2； 解：（1）分析整体，作示力图  0)(iB FM： F 2F FN 2F FN A E C D B FA FB FAB FBC W B E FN1 FN3 FN2 β (c) 041088AF 40kNAF  （2）取部分分析，示力图见（b）  0)(iC FM： 02442.22qFFAN 2(404402)36.36kN2.2NF 3262236.36 1031.62MPa1150 10NFA杆 （3）分析铰 E，示力图见（c）  0ixF： 0sin12NNFF 22122140.65kN2NNFF 3161137.96 1035.3MPa1150 10NFA杆 2-3 求下列各杆内的最大正应力。 （3）图(c)为变截面拉杆，上段 AB 的横截面积为 40mm2，下段 BC 的横截面积为 30mm2，杆材料的 ρg=78kN/m3。 解：1.作轴力图，BC 段最大轴力在 B 处 6N120.5 30 107812.0kNBF AB 段最大轴力在 A 处 6N12 12(0.5 300.540) 107812.0kNAF C FA q FCy FCx FN2 (b) A B C 12.0 12.0 FN (kN) 3N2612.0 10400MPa30mm30 10BBF 3N2612.0 10300MPa40mm40 10AAF 杆件最大正应力为400MPa，发生在B 截面。 2-4 一直径为15mm，标距为200mm 的合金钢杆，比例极限内进行拉伸试验，当轴向荷载从零缓慢地增加58.4kN 时，杆伸长了0.9mm，直径缩小了0.022mm，确定材料的弹性模量E、泊松比ν。 解：加载至 58.4kN 时，杆件横截面中心正应力为 3N2458.4 10330.48MPa1.5104FA＝ 线应变：333Δ0.9 104.5 10200 10ll 弹性模量：33330.48MPa73.4 10 MPa4.5 10E  侧向线应变：310467.115022.0＝， 泊松比：,0.326 2-6 图示短柱，上段为钢制，长200mm，截面尺寸为100×100mm2；下段为铝制，长300mm，截面尺寸为200×200mm2。当柱顶受 F 力作用时，柱子总长度减少了0.4mm，试求 F 值。已知 E钢=200GPa，E铝=70GPa。 解：柱中的轴力都为...