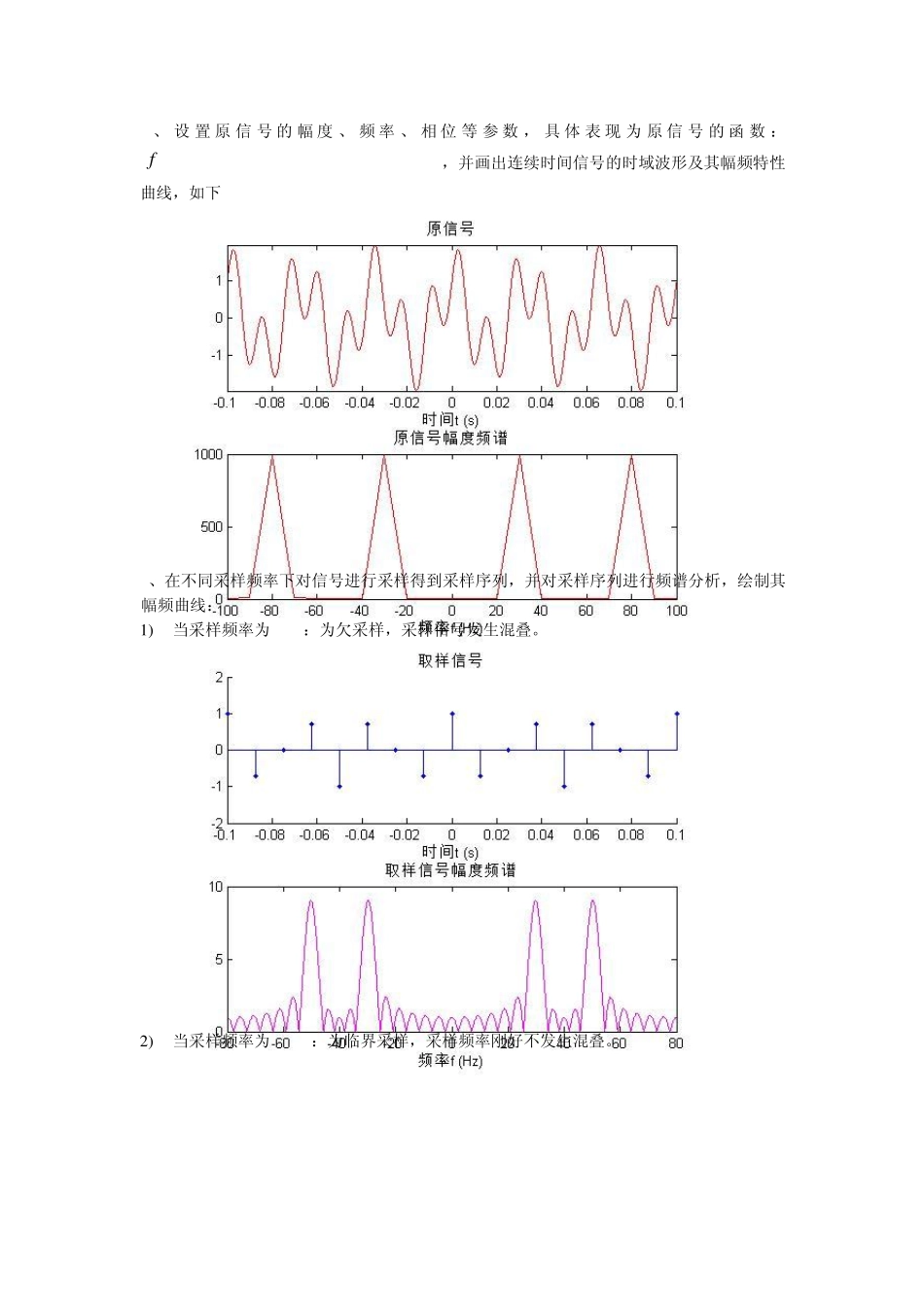
通信原理实验报告 2012-2013( 上 ) 姓名 学号 专业 实验一:MATLAB验证低通抽样定理 实验目的 1、掌握抽样定理的工作原理。 2、通过 MATLAB编程实现对抽样定理的验证,加深抽样定理的理解。同时训练应用计算机分析问题的能力。 3、了解 MATLAB软件,学习应用 MATLAB软件的仿真技术。它主要侧重于某些理论知识的灵活运用,以及一些关键命令的掌握,理解,分析等。 4、计算在临界采样、过采样、欠采样三种不同条件下恢复信号的误差,并由此总结采样频率对信号恢复产生误差的影响,从而验证时域采样定理。 程序设计 整个程序由三部分组成:主函数、采样函数、恢复函数。 主函数中: f1='sin(2*pi*80*t)+cos(2*pi*30*t)';//用来画出原信号 fs0=caiyang(f1,x); //用来获得采样信号 fr0=huifu(fs0,x); //用来获得恢复信号 fs0和 fr0中的x即为人为所设定的采样频率。 采样函数中: 初始设定fs0=10000; tp=0.1; f=[fs0*k2/m2,fs0*k1/m1]; //设置原信号的频率数组 FX1=fx1*exp(-j*[1:length(fx1)]'*w);//求原信号的离散时间傅里叶变换。 axis([min(t),max(t),min(fx1),max(fx1)]) ;//画原信号幅度频谱 axis([-100,100,0,max(abs(FX1))+5]) ;//对信号进行采样 Ts=1/fs; //采样周期 t1=-tp:Ts:tp; //采样时间序列 f1=[fs*k2/m2,fs*k1/m1]; //设置采样信号的频率数组 t=t1; //变量替换 fz=eval(fy); // 获取采样序 FZ=fz*exp(-j*[1:length(fz)]'*w); //采样信号的离散时间傅里叶变换 恢复函数中: T=1/fs; dt=T/10; tp=0.1; fh=fz*sinc(fs*TMN); //由采样信号恢复原信号 w=[-2*pi*k2/m2,2*pi*k1/m1]; FH=fh*exp(-j*[1:length(fh)]'*w); //恢复后的信号的离散时间傅里叶变换 line([min(t),max(t)],[0,0]) //画重构信号的幅度频谱 实验步骤 1、安装 MATLAB6.5软件 2、学习简单编程,画图 plot(x,y)函数等 3、 设 置 原 信 号 的 幅 度 、 频 率 、 相 位 等 参 数 , 具 体 表 现 为 原 信 号 的 函 数 :f (x)=sin(2*pi*80*t)+ cos(2*pi*30*t),并画出连续时间信号的时域波形及其幅频特性曲线,如下: 4、在不同采样频率下对信号进行采样得到采样序列,并对采样序列进行频谱分析,绘制其幅频曲线: 1 ) 当采样频率为80Hz:为欠采样,采样信号发生混叠。 2 ) 当采样频率为160Hz:为临界采样,采样频率刚好不发生混叠。 3 ) 采样频率为1...