极值点偏移12极值点偏移定理

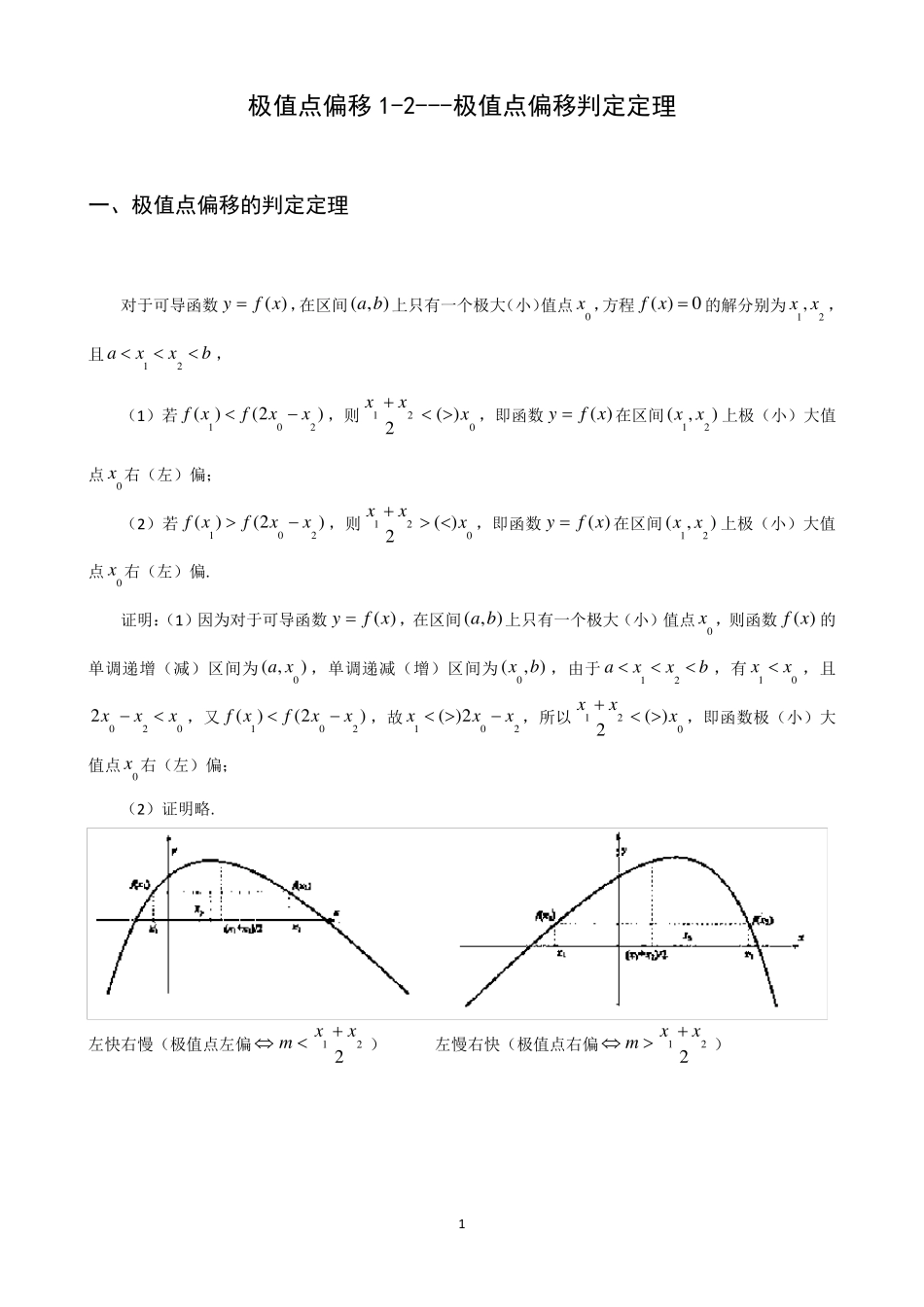
1 极值点偏移1-2---极值点偏移判定定理 一、极值点偏移的判定定理 对于可导函数 )(xfy，在区间),(ba上只有一个极大（小）值点0x ，方程0)(xf的解分别为21 , xx，且bxxa21， （1）若)2()(201xxfxf，则021)(2xxx，即函数)(xfy在区间),(21 xx上极（小）大值点0x 右（左）偏； （2）若)2()(201xxfxf，则021)(2xxx，即函数)(xfy在区间),(21 xx上极（小）大值点0x 右（左）偏. 证明：（1）因为对于可导函数)(xfy，在区间),(ba上只有一个极大（小）值点0x ，则函数)(xf的单调递增（减）区间为),(0xa，单调递减（增）区间为),(0 bx，由于bxxa21，有01xx ，且0202xxx，又)2()(201xxfxf，故2012)(xxx，所以021)(2xxx，即函数极（小）大值点0x 右（左）偏； （2）证明略. 左快右慢（极值点左偏221xxm） 左慢右快（极值点右偏221xxm） 2 左快右慢（极值点左偏221xxm） 左慢右快（极值点右偏221xxm） 二、运用判定定理判定极值点偏移的方法 1、方法概述： （1）求出函数)(xf的极值点0x ； （2）构造一元差函数)()()(00xxfxxfxF； （3）确定函数)(xF的单调性； （4）结合0)0(F，判断)(xF的符号，从而确定)(0xxf、)(0xxf的大小关系. 口诀：极值偏离对称轴，构造函数觅行踪；四个步骤环相扣，两次单调紧跟随. 2、抽化模型 答题模板：若已知函数)(xf满足)()(21xfxf，0x 为函数)(xf的极值点，求证：0212 xxx. （1）讨论函数)(xf的单调性并求出)(xf的极值点0x ； 假设此处)(xf在),(0x上单调递减，在),(0 x上单调递增. （2）构造)()()(00xxfxxfxF； 注：此处根据题意需要还可以构造成)2()()(0xxfxfxF的形式. （3）通过求导)(' xF讨论)(xF的单调性，判断出)(xF在某段区间上的正负，并得出)(0xxf与)(0xxf的大小关系； 假设此处)(xF在),0(  上单调递增，那么我们便可得出0)()()()(000xfxfxFxF，从而得到：0xx时，)()(00xxfxxf. （4）不妨设201xxx，通过)(xf的单调性，)()(21xfxf，)(0xxf与)(0xxf的大小关系得出 3 结论； 接上述情况，由于0xx 时，)()(00xxfxxf且201xxx，)()(21xfxf， 故)2()]([)]([)()(2002002021xxfxxxfxxxfxfxf，又因为01xx ， 0202xxx且)(xf在 ),(0x上单调递减，从而得到...