极坐标与参数方程高考经典题型归纳总结

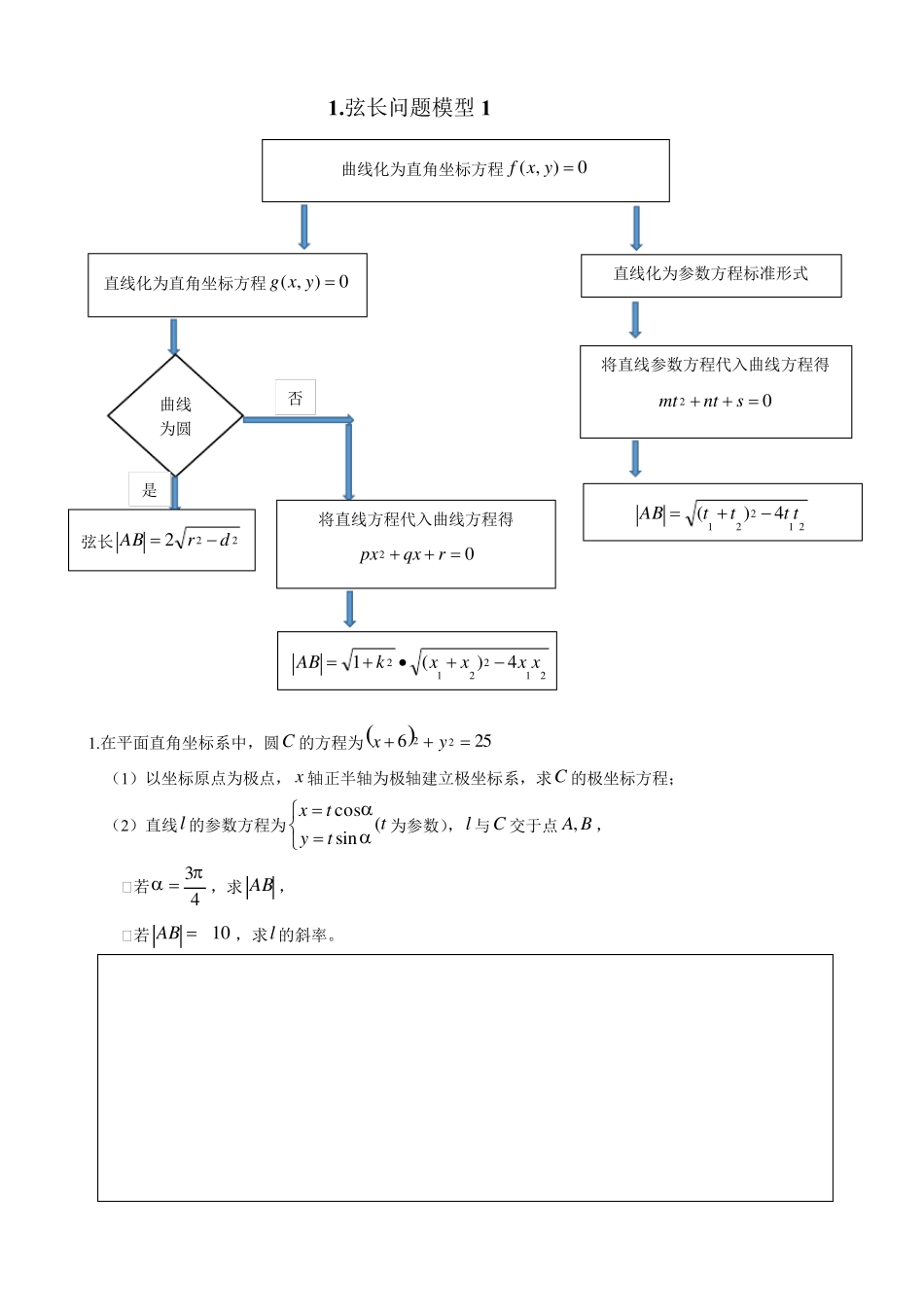
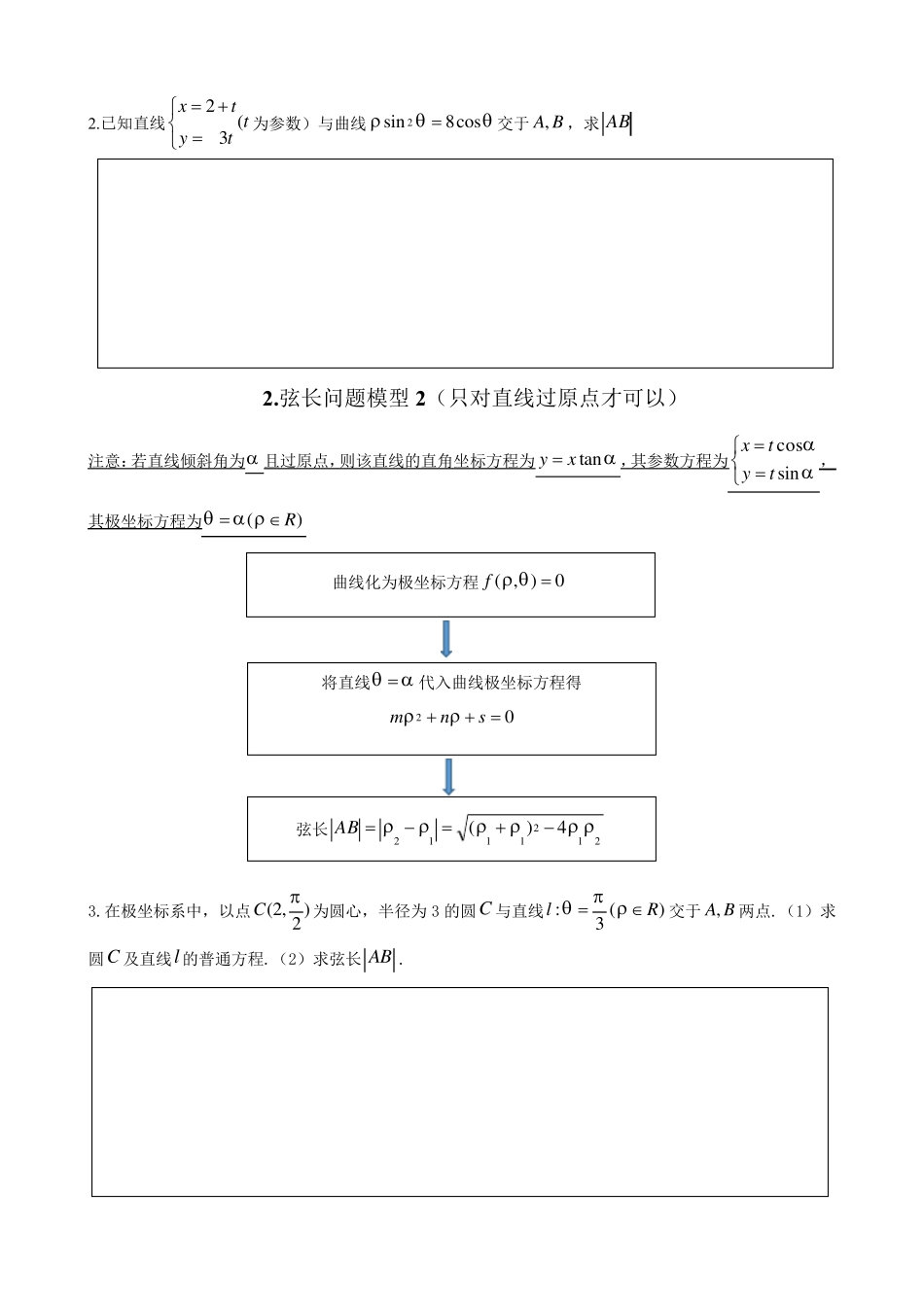
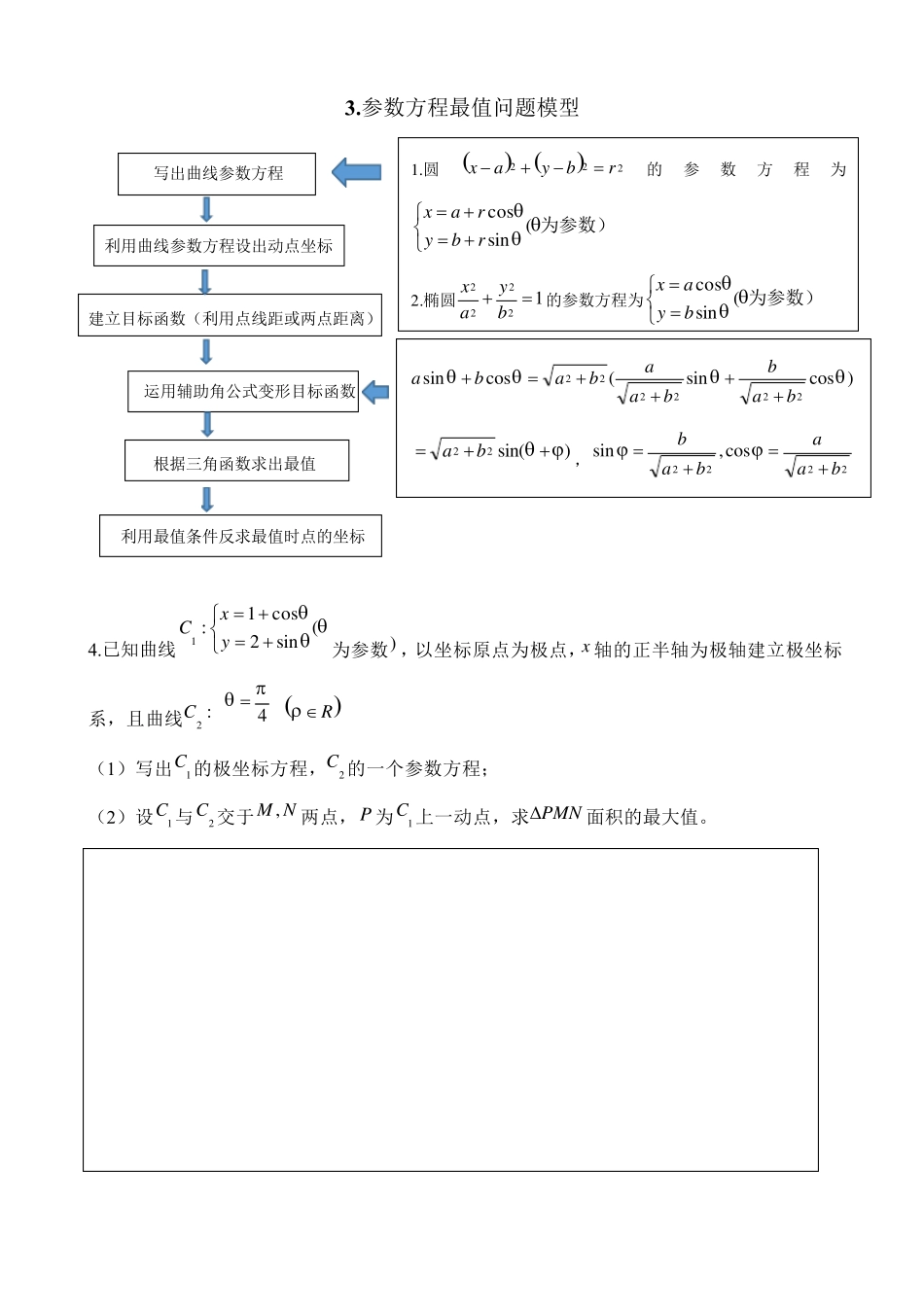
1 .弦长问题模型1 1.在平面直角坐标系中，圆C 的方程为25622yx （1）以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求C 的极坐标方程； （2）直线l 的参数方程为ttytx(sincos为参数），l 与C 交于点BA,， ① 若43 ，求AB ， ① 若 10AB，求l 的斜率。 曲线化为直角坐标方程0),(yxf 直线化为参数方程标准形式 直线化为直角坐标方程0),(yxg 将直线参数方程代入曲线方程得 02sntmt 曲线为圆 否 是 212214)(ttttAB 将直线方程代入曲线方程得02rqxpx 弦长222drAB 2122124)(1xxxxkAB• 2 .已知直线ttytx(32为参数）与曲线cos8sin 2交于BA,，求 AB 2 .弦长问题模型 2 （只对直线过原点才可以） 注意：若直线倾斜角为 且过原点，则该直线的直角坐标方程为tanxy ，其参数方程为sincostytx， 其极坐标方程为)(R 3.在极坐标系中，以点(2,)2C为圆心，半径为3 的圆C 与直线:()3lR交于,A B 两点.（1）求圆C 及直线l 的普通方程.（2）求弦长 AB . 曲线化为极坐标方程0),(f 将直线 代入曲线极坐标方程得02snm 弦长21211124)(AB 1.圆222rbyax的参数方程为为参数）(sincosrbyrax 2.椭圆12222 byax的参数方程为为参数）(sincosbyax )cossin(cossin222222babbaababa )sin(22 ba，2222cos,sinbaabab 3 .参数方程最值问题模型 写出曲线参数方程 利用曲线参数方程设出动点坐标 建立目标函数（利用点线距或两点距离） 运用辅助角公式变形目标函数 根据三角函数求出最值 利用最值条件反求最值时点的坐标 4.已知曲线 (sin2cos1:1 yxC为参数) ，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，且曲线:2C 4  R （1）写出1C 的极坐标方程，2C 的一个参数方程； （2）设1C 与2C 交于NM ,两点，P 为1C 上一动点，求PMN面积的最大值。 如何写直线参数方程的标准形式：(思考：如何判断是否为标准形式） （1）取直线上一个定点（如果题目有现成的就用题目所给的）00, yx （2）求出直线斜率： tank (3)求出（知一求二) cos,sin (4）...