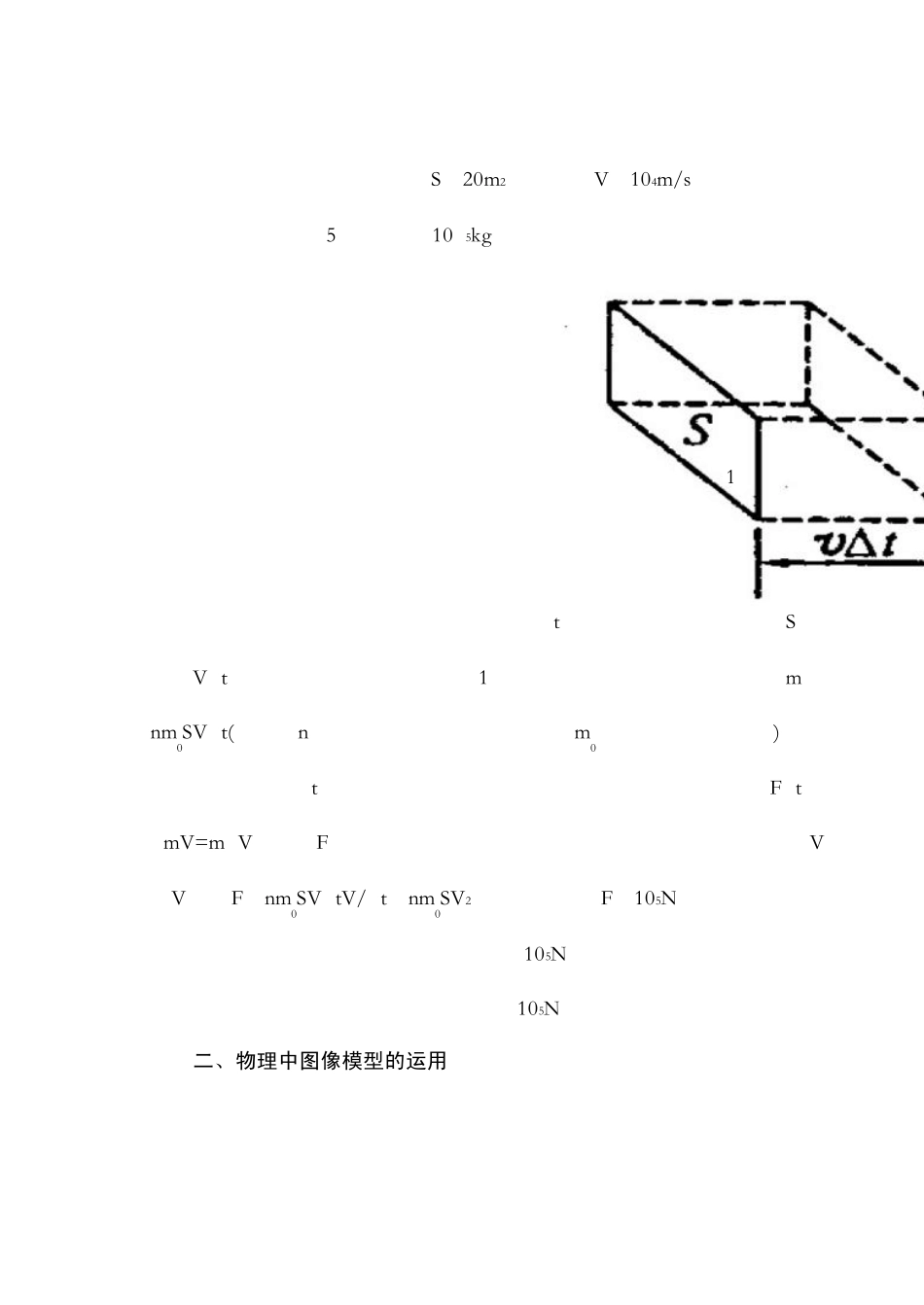
构建物理模型,培养提高解题能力 南平一中 郑剑榕 自然界中任何事物与其他许多事物之间总是存在着千丝万缕的联系,并处在不断的变化之中。面对复杂多变的自然界,人们在研究物理问题时,常常是遵循这样一条重要的方法论原则,即从简到繁,先易后难,循序渐进,逐步深入。基于这样的一个思维过程,在物理学中,人们就建立了“物理模型”。物理模型是物理思想的产物,是研究物理的一种方法,是在抓住主要因素、忽略次要因素的基础上建立起来的。因而,它能具体、形象、生动、深刻地反映事物的本质和主流。如何帮助学生正确构建和运用物理模型,培养学生的思维能力和解决实际问题的能力,在教学实践中,本人注重通过图像模型、数学模型、系统转换模型等多种物理模型的运用,启发、引导学生合理建立和运用物理模型,并逐步熟悉和掌握这种科学研究的思维方法,在解题过程中,充分运用和发挥物理模型的优势,化繁为简,化动为静,化抽象为具体,帮助学生理解解题思路,拓展思维,提高分析问题和解决问题的能力,获得事半功倍的效果。 一、物理中的数学模型的运用 客观世界的一切规律,原则上都可以在数学中找到它们的表现形式。在建造物理模型的同时,也在不断地建造表现物理状态及物理过程规律的数学模型。我们必须让学生强化这一见解。当然,由于物理模型是客观实体的一种近似,因此以物理模型为描述对象的数学模型,只能是客观实体的近似的定量描述。 例:宇宙飞船横截面积为 S=20m2,以速度 V=104m/s 的速度匀速穿过每立方米平均有 5 个质量为 10-5kg 的微尘空间,求飞船发动机的推力。 解析:飞船与微尘碰撞时,微尘的运动有多种可能,或者向各个方向被弹开,或者附着在飞船上。微尘与飞船相对速度很大,从抓主要矛盾角度来看,微尘“嵌入”飞船外壳的可能性最大。于是我们可以假设与飞船碰撞的微粒“全部”附着在飞船上,与飞船具有共同的速度,而飞船的速度远大于微粒的速度,故把微粒可视为静止的,则可假设飞船在时间 Δt 内“扫过”的空间是以 S 为底、VΔt 为高的一个柱体,如图(1)所示。该区域内微尘的质量 m=nm0SVΔt(其中:n 为单位体积内微尘的个数,m0 为每个微尘的质量)。在一个较小的时间 t 内,可以忽略微尘的重力,应用动量定理可知 FΔt=ΔmV=mΔV,其中 F 为飞船对微尘的作用力。假设微尘初速度为零,则 ΔV=V,故 F=nm0SVΔtV/Δt=nm0SV2。代入数据得 F=105N,根据牛顿第三定律可知,微...