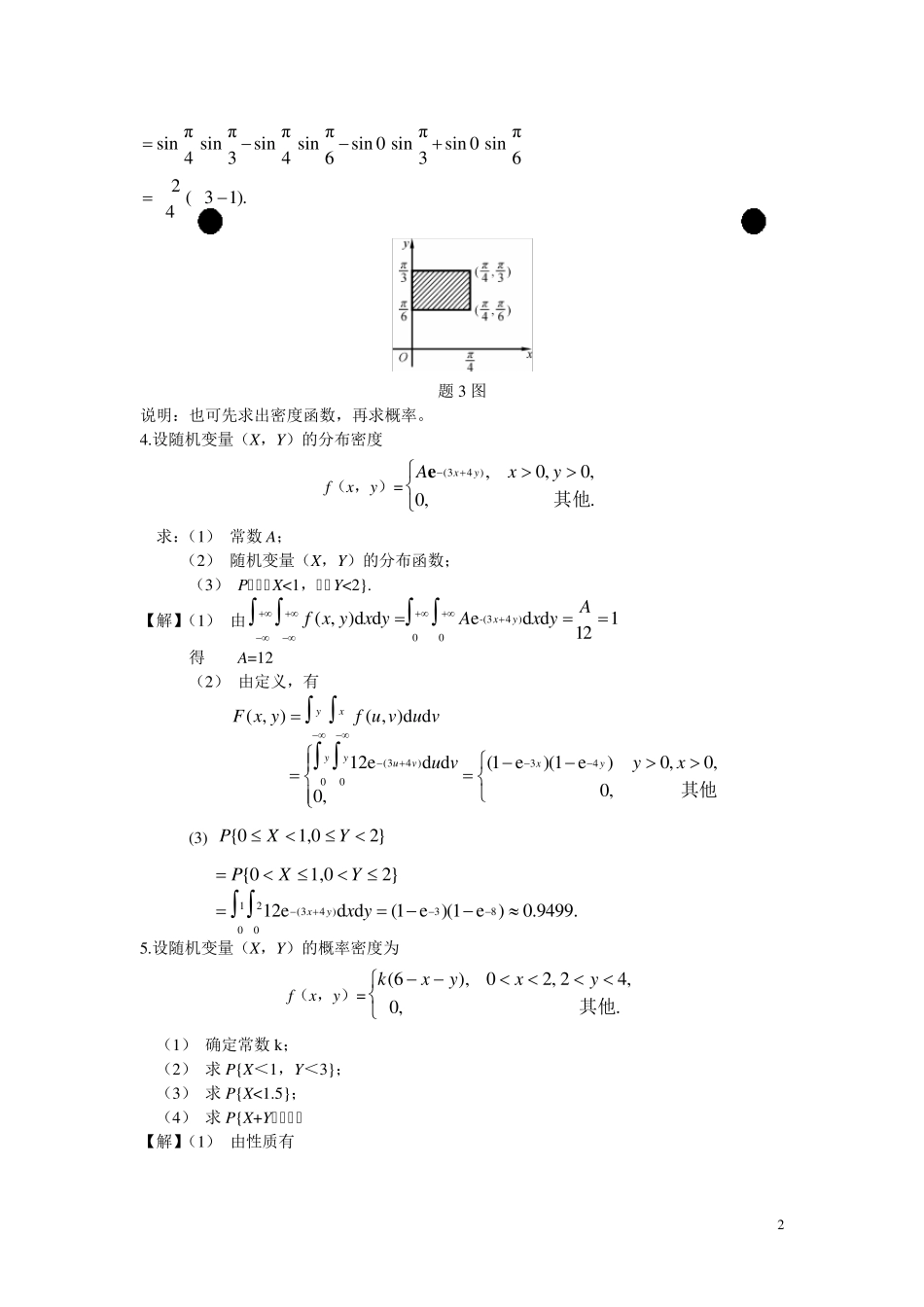
1 习题三 1.将一硬币抛掷三次,以X 表示在三次中出现正面的次数,以Y 表示三次中出现正面次数与出现反面次数之差的绝对值.试写出X 和Y 的联合分布律. 【解】X 和Y 的联合分布律如表: 0 1 2 3 1 0 131113C2228 23111C3/8222 0 3 18 0 0 11112228 2.盒子里装有3 只黑球、2 只红球、2 只白球,在其中任取 4 只球,以X 表示取到黑球的只数,以Y 表示取到红球的只数.求 X 和Y 的联合分布律. 【解】X 和Y 的联合分布律如表: 0 1 2 3 0 0 0 223247C C3C35 313247C C2C35 1 0 11232247C C C6C35 21132247C C C12C35 313247C C2C35 2 P(0 黑,2 红,2 白)= 2242271C C / C35 12132247C C C6C35 223247C C3C35 0 3.设二维随机变量(X,Y)的联合分布函数为 F(x,y)=.,020,20,sinsin其他ππyxyx 求二维随机变量(X,Y)在长方形域36,40πππyx内的概率. 【解】如图π ππ{0,}(3.2)4 63PXY公式 π ππ πππ(,)(,)(0,)(0,)4 34 636FFFF X Y X Y 2 ππππππsinsinsinsinsin 0 sinsin 0 sin4346362 ( 31).4 题3 图 说明:也可先求出密度函数,再求概率。 4.设随机变量(X,Y)的分布密度 f(x,y)=.,0,0,0,)43(其他yxAyxe 求:(1) 常数A; (2) 随机变量(X,Y)的分布函数; (3) P{0≤X<1,0≤Y<2}. 【解】(1) 由-(34 )00( , )d ded d112xyAf x yx yAx y 得 A=12 (2) 由定义,有 ( , )( , )d dyxF x yf u vu v (34 )340012ed d(1 e)(1 e)0,0,0,0,yyuvxyu vyx 其他 (3) {01,02}PXY 12(34 )3800{01,02}12ed d(1 e )(1 e )0.9499.xyPXYx y 5.设随机变量(X,Y)的概率密度为 f(x,y)=.,0,42,20),6(其他yxyxk (1) 确定常数k; (2) 求P{X<1,Y<3}; (3) 求P{X<1.5}; (4) 求P{X+Y≤4}. 【解】(1) 由性质有 3 2402( , )d d(6)d d81,f x yx ykxyy xk 故 18R (2) 13{1,3}( , )d dP XYf x yy x...