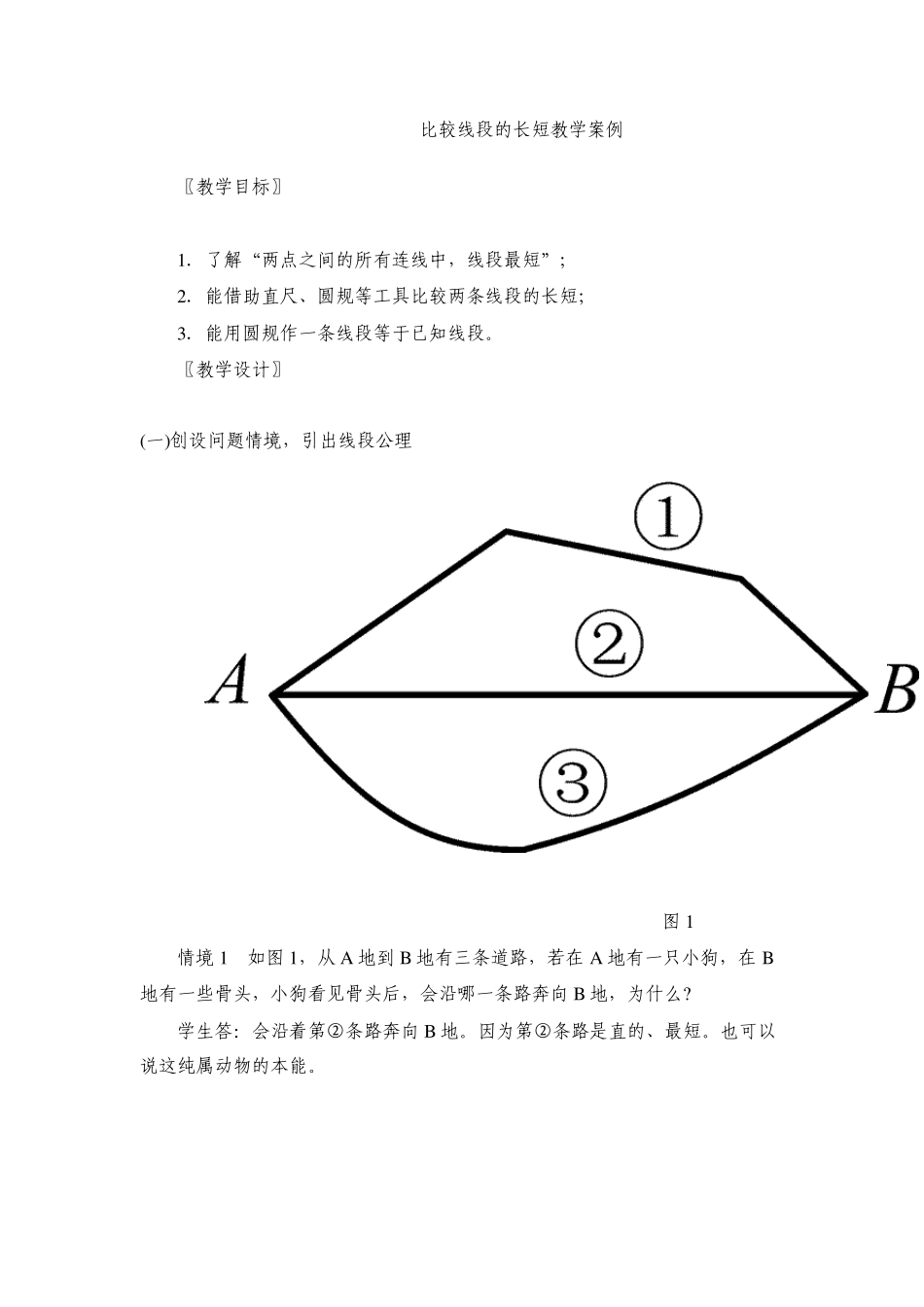
比较线段的长短教学案例 〖教学目标〗 1.了解“两点之间的所有连线中,线段最短”; 2.能借助直尺、圆规等工具比较两条线段的长短; 3.能用圆规作一条线段等于已知线段。 〖教学设计〗 (一)创设问题情境,引出线段公理 图 1 情境 1 如图 1,从 A 地到 B 地有三条道路,若在 A 地有一只小狗,在 B地有一些骨头,小狗看见骨头后,会沿哪一条路奔向 B 地,为什么? 学生答:会沿着第②条路奔向 B 地。因为第②条路是直的、最短。也可以说这纯属动物的本能。 图2 情境2 如图2,从教室A 地到图书馆B,总有少数同学不走人行道而横穿草坪,这是为什么呢? 学生答:因为走的路程最短。 教师指出:1.两种情境所揭示的原理是一样的,都说明了这样一个公理:两点之间的所有连线中,线段最短,我们把这个公理叫做线段公理。 用《几何画板》验证线段公理:用《几何画板》中度量菜单里的长度命令,量出情境1 中三条路线的长度,可以发现道路②最短。 2.两点之间线段的长度,叫做这两点之间的距离。 在情境1 中,道路②的长度就是A,B 两地的距离。 (二)四名学生为一组,通过合作解决实际问题 1.通过情境1 的学习,可能有的同学会问:“难道小狗也懂数学吗?”其实,小狗不懂数学。小狗沿着第②条路奔向 B 地,这纯属动物的本能,纯属几何直觉,动物和人都有几何直觉。人类会从实际问题中总结和抽象出数学理论,并主动地应用于实践,这是人类优于动物的地方。根据所学知识,你们能解决下面问题吗?请以小组为单位,通过合作解答此题。 图 3 问题 如图 3,A,B 是河流 n两旁的两个村庄,现要在河边建一个引水站向两村供水,问引水站建在什么地方才能使所需的管道最短?请在图中标出引水站的位置 P,并说明你的理由。 (答案:连接 AB 交直线 n于点 P,点 P 的位置就是引水站的位置。) 2.完成此题的小组,派一名代表通过多媒体展示答案。 3.教师做总结性发言,点评各小组的表现。 4.教师用《几何画板》验证答案。具体方法如下: 在直线 n上任取一点 P,连接 PA,PB,AB,用《几何画板》中度量菜单里的长度命令,度量出 PA,PB,AB 的长度,然后计算出 PA+PB。拖动点 P,可以观察到:当点 P 与线段 AB 和直线 n的交点重合时,PA+PB 最小。 (三)想一想 情境2 中,少数同学的做法对吗?为什么? 学生答:不对,因为他们践踏了草坪。 教师:我们在运用科学知识为人类服务的时候,应遵纪...