2025年高中数学必修4三角函数知识点归纳总结

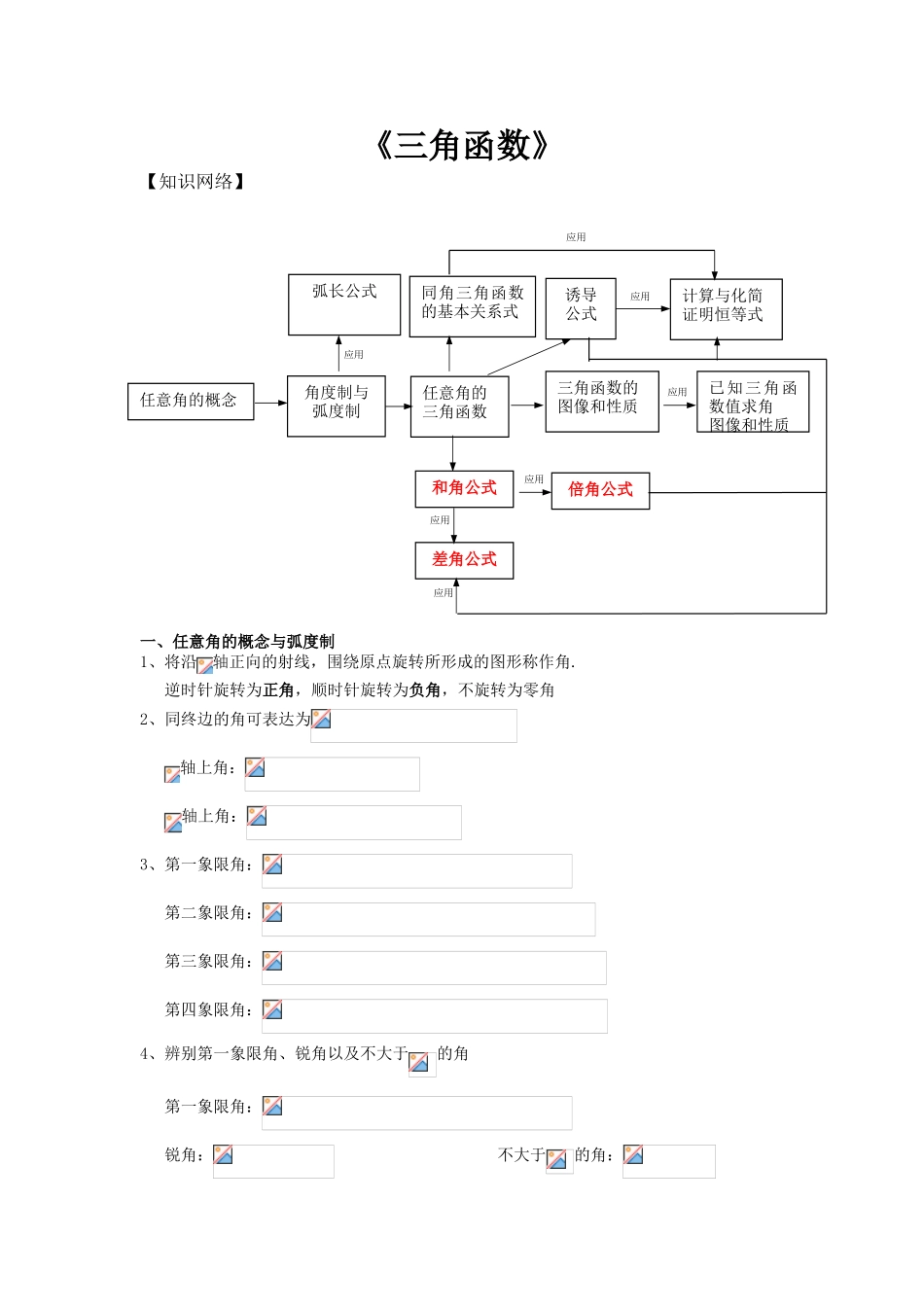
《三角函数》【知识网络】一、任意角的概念与弧度制1、将沿轴正向的射线，围绕原点旋转所形成的图形称作角. 逆时针旋转为正角，顺时针旋转为负角，不旋转为零角2、同终边的角可表达为轴上角：轴上角：3、第一象限角： 第二象限角： 第三象限角： 第四象限角：4、辨别第一象限角、锐角以及不大于的角 第一象限角： 锐角： 不大于的角：任意角的概念弧长公式角度制与弧度制同角三角函数的基本关系式诱导公式计算与化简证明恒等式任意角的三角函数三角函数的图像和性质已知三角函数值求角图像和性质和角公式倍角公式差角公式应用应用应用应用应用应用应用5、若为第二象限角，那么为第几象限角？ 因此在第一、三象限6、弧度制：弧长等于半径时，所对的圆心角为 弧度的圆心角，记作.7、角度与弧度的转化： 8、角度与弧度对应表：角度弧度9、弧长与面积计算公式 弧长：；面积：，注意：这里的均为弧度制.二、任意角的三角函数1、正弦：；余弦；正切 其中为角终边上任意点坐标，.2、三角函数值对应表：3、三角函数在各象限中的符号口诀：一全正，二正弦，三正切，四余弦.（简记为“全 s t c”）度弧度无无 第一象限： sin0,cos0,tan0,第二象限： sin  0,cos0,tan0,第三象限： sin0,cos0,tan  0,第四象限： sin0,cos  0,tan0,4、三角函数线设任意角的顶点在原点，始边与轴非负半轴重叠，终边与单位圆相交与，过作轴的垂线，垂足为；过点作单位圆的切线，它与角的终边或其反向延长线交于点 T.由四个图看出：（Ⅳ）（Ⅱ）（Ⅰ）（Ⅲ）当角的终边不在坐标轴上时，有向线段，于是有， ，．我们就分别称有向线段为正弦线、余弦线、正切线。5、同角三角函数基本关系式(，，，三式之间可以互相表达)6、诱导公式口诀：奇变偶不变,符号看象限(所谓奇偶指的是中整数的奇偶性，把看作锐角)；.①.公式（一）：与；；②.公式（二）：与；；③.公式（三）：与；；④.公式（四）：与；；⑤.公式（五）：与；；⑥.公式（六）：与；；⑦.公式（七）：与；；⑧.公式（八）：与；；三、三角函数的图像与性质1、将函数的图象上所有的点，向左（右）平移个单位长度，得到函数的图象；再将函数的图象上所有点的横坐标伸长（缩短）到 本 来 的倍 （ 纵 坐 标 不 变 ） ， 得 到 函 数的 图 象 ； 再 将 函 数的图象上所有点的纵坐标伸长（缩短）到本来的倍（横坐标不变），得到函数的图象。2、函数的性...