电路第四版答案(第四章)

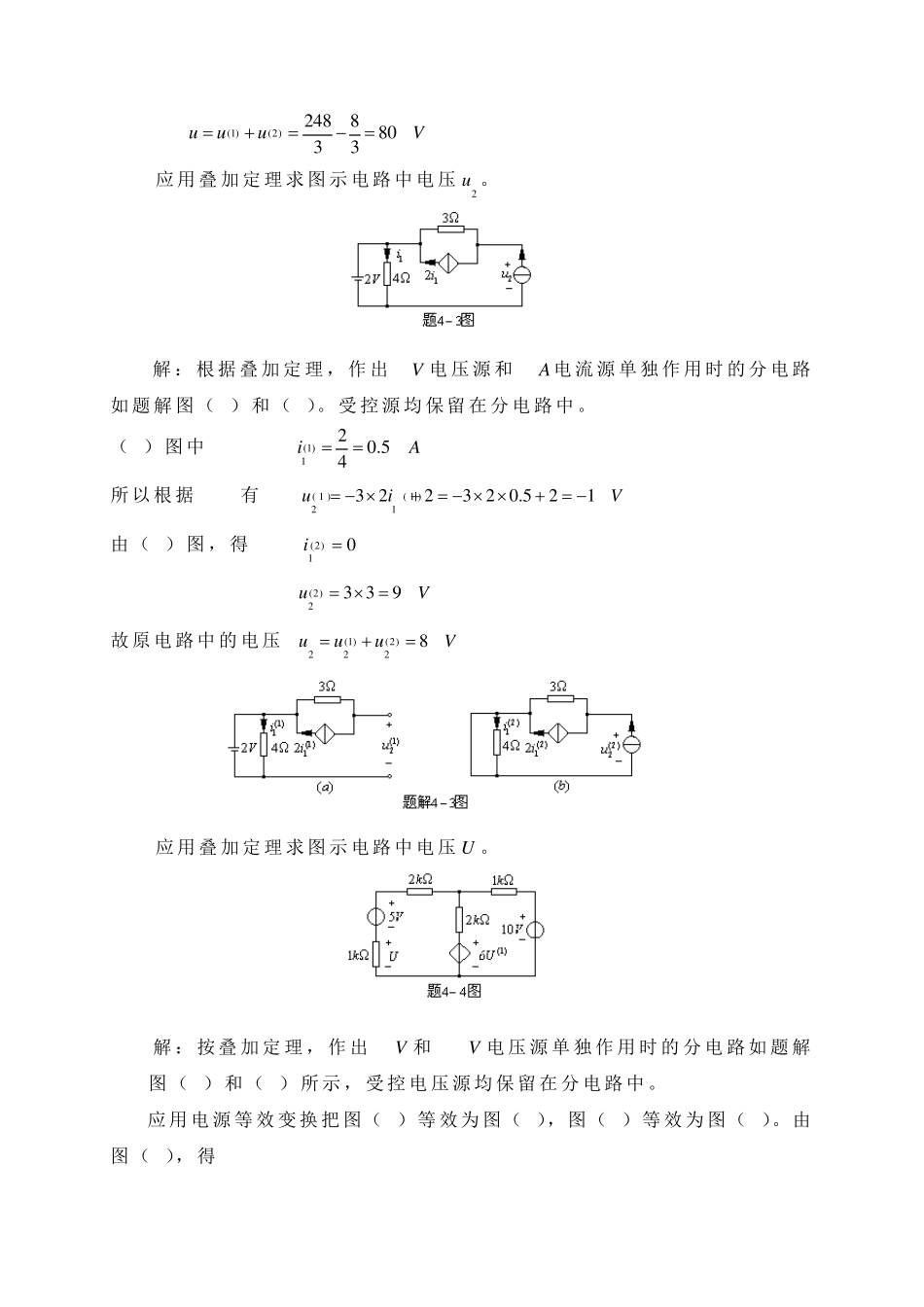
第四章 电路定理 电路定理是电路理论的重要组成部分，为我们求解电路问题提供了另一种分析方法，这些方法具有比较灵活，变换形式多样，目的性强的特点。因此相对来说比第三章中的方程式法较难掌握一些，但应用正确，将使一些看似复杂的问题的求解过程变得非常简单。应用定理分析电路问题必须做到理解其内容，注意使用的范围、 条 件 ，熟 练 掌握使用的方法和 步 骤 。需 要指 出 ，在 很 多问题中定理和 方程法往 往 又 是结 合 使用的。 4-1 应用叠 加 定理求图 示 电路中电压abu。 解：首 先 画 出 两 个 电源 单独 作 用式的分电路入 题解4-1图（ a）和（ b）所 示 。 对（ a） 图 应用结 点电压 法可 得 1sin5)121311(1tun  解得 15sin3sin53ntutV (1)111113sinsin2 133nabnuuuttV  对（ b） 图 ，应用电阻 的分流 公 式有 1132 111135tteieA 所 以 (2)110.25ttabuieeV   故 由 叠 加 定理得 ( 1 )( 2 ) si n0 . 2ta ba ba buuuteV 4-2 应用叠加定理求图示电路中电压u 。 解 ： 画 出 电源 分 别 作 用的 分 电路如 题 解 （ a） 和 （ b） 所 示。 对 （ a） 图应用结 点 电压法 有 1 05 0281 3 6)1 014 01281(1nu 解 得 (1 )11 3 .650 .10 .0 2 50 .1nuu 1 8 .62 4 88 2 .6 6 70 .2 2 53V 对 （ b） 图， 应用电阻 串 并 联 化 简 方 法 ， 可 求得 1 04 02(8)3 21 61 04 0331 04 01 83(8)21 04 0siuV   (2 )1 6182323siuuV   所 以 ， 由 叠加定理得 原 电路的 u 为 (1 )(2 )2 4 888 033uuuV 4-3 应用叠加定理求图示电路中电压2u 。 解 ： 根 据 叠加定理， 作 出 2V 电压源 和 3A电流 源 单 独 作 用时 的 分 电路如 题 解 图（ a） 和 （ b）。 受 控 源 均 保 留 在 分 电路中。 （ a） 图中 (1 )120 .54iA 所 以 根 据 KVL有 ( 1 )( 1 )21322320 .521uiV       由 （ b） 图， 得 0)2(1i (2 )2339uV  故 原 电路中的 电压 (1 )(2 )2228uuuV 4-4...