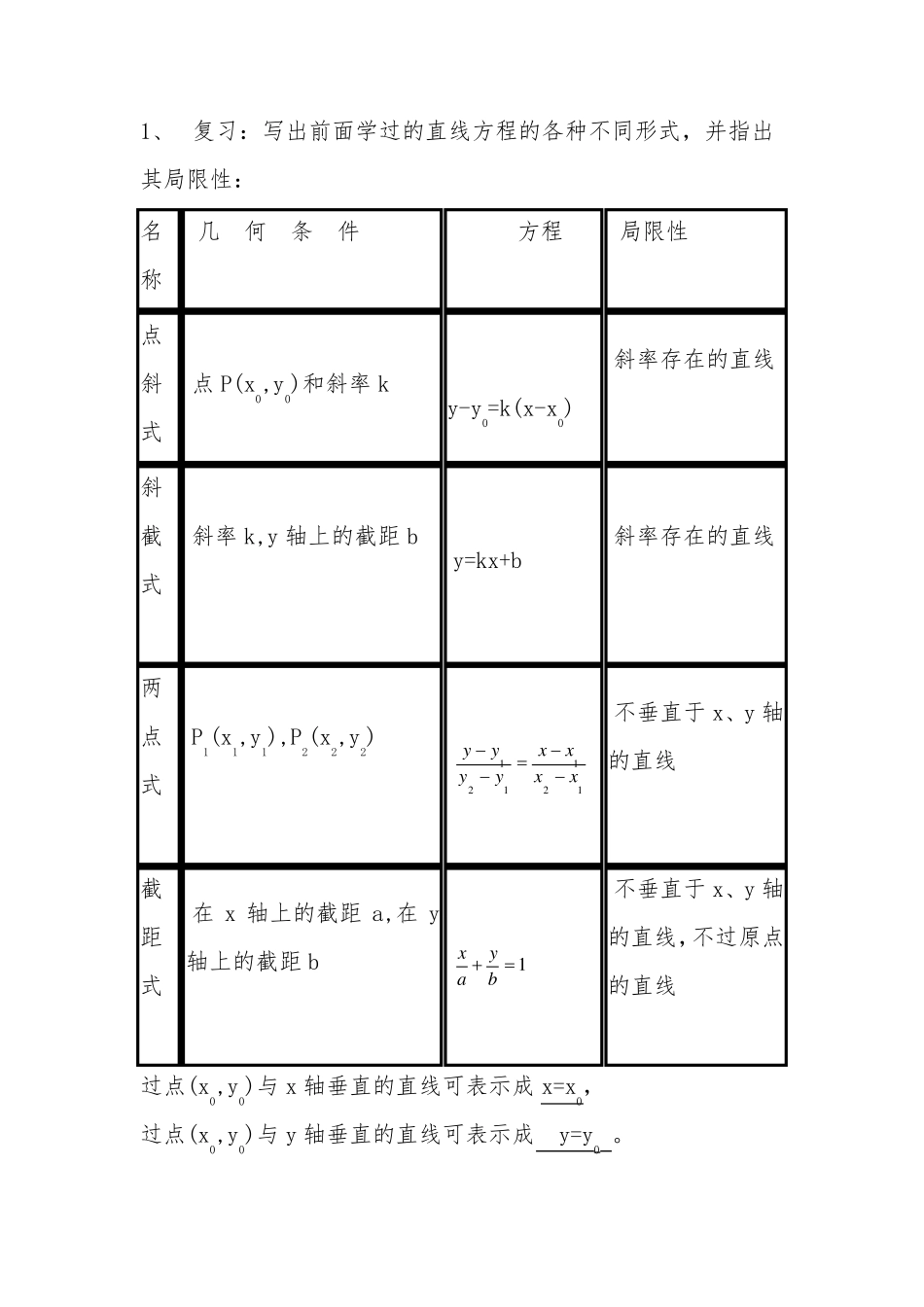
3.2.3 直线的一般式方程(教案) 教学目标: 1、知识与能力: ⑴掌握直线方程的一般式Ax+By+C=0 的特征(A、B 不同时为 0) ⑵能将直线方程的五种形式进行转化,并明确各种形式中的一些几何量(斜率、截距等); 2、过程与方法: ⑴主动参与探究直线和二元一次方程关系的数学活动,通过观察、推理、探究获得直线方程的一般式。 ⑵学会分类讨论及掌握讨论的分界点; 3、情感、态度与价值观: 体验数学发现和探索的历程,发展创新意识 教学重点: 直线方程一般式Ax+By+C=0(A、B 不同时为 0)的理解 教学难点: ⑴直线方程一般式Ax+By+C=0(A、B 不同时为 0)与二元一次方程关系的深入理解 ⑵直线方程一般式Ax+By+C=0(A、B 不同时为 0)的应用。 教学方法: 引导探究法、讨论法 教学过程: 创设情境,引入新课: 1、 复习:写出前面学过的直线方程的各种不同形式,并指出其局限性: 名 称 几 何 条 件 方程 局限性 点斜式 点 P(x0,y0)和斜率 k y-y0=k(x-x0) 斜率存在的直线 斜截式 斜率 k,y 轴上的截距 b y=kx+b 斜率存在的直线 两点式 P1(x1,y1),P2(x2,y2) 121121xxxxyyyy 不垂直于 x、y 轴的直线 截距式 在 x 轴上的截距 a,在 y轴上的截距 b 1 byax 不垂直于 x、y 轴的直线,不过原点的直线 过点(x0,y0)与 x 轴垂直的直线可表示成 x=x0, 过点(x0,y0)与 y 轴垂直的直线可表示成 y=y0 。 2、 问题:上述四种直线方程的表示形式都有其局限性,是否存在一种更为完美的代数形式可以表示平面中的所有直线? 提 示:上述四种形式的直线方程有何共同特征?能否整理成统一形式?(这些方程都是关于 x、y 的二元一次方程) 猜 测:直线和二元一次方程有着一定的关系。 新课探究: 问题: (1).过点(2,1),斜率为 2 的直线的方程是 y-1=2(x-2), (2).过点(2,1),斜率为 0 的直线方程是 y=1, (3).过点(2,1),斜率不存在的直线的方程是 x=2, 思考 1 :以上方程是否都可以用 Ax+By+C=0 表示?任意一条直线是否都可以用二元一次方程 Ax+By+C=0(A、B 不同时为 0)来表示? 答: 2x-y-3=0 y-1=0 x-2=0 在平面直角坐标系中,每一条直线有斜率 k 存在和 k 不存在两种情况下,直线方程可分别写为 ykxb 和1xx两种形式,它们又都可以变形为 Ax+By+C=0(A、B 不同时为 0)的形式,即:直线 Ax+By+C=0(A、B 不...