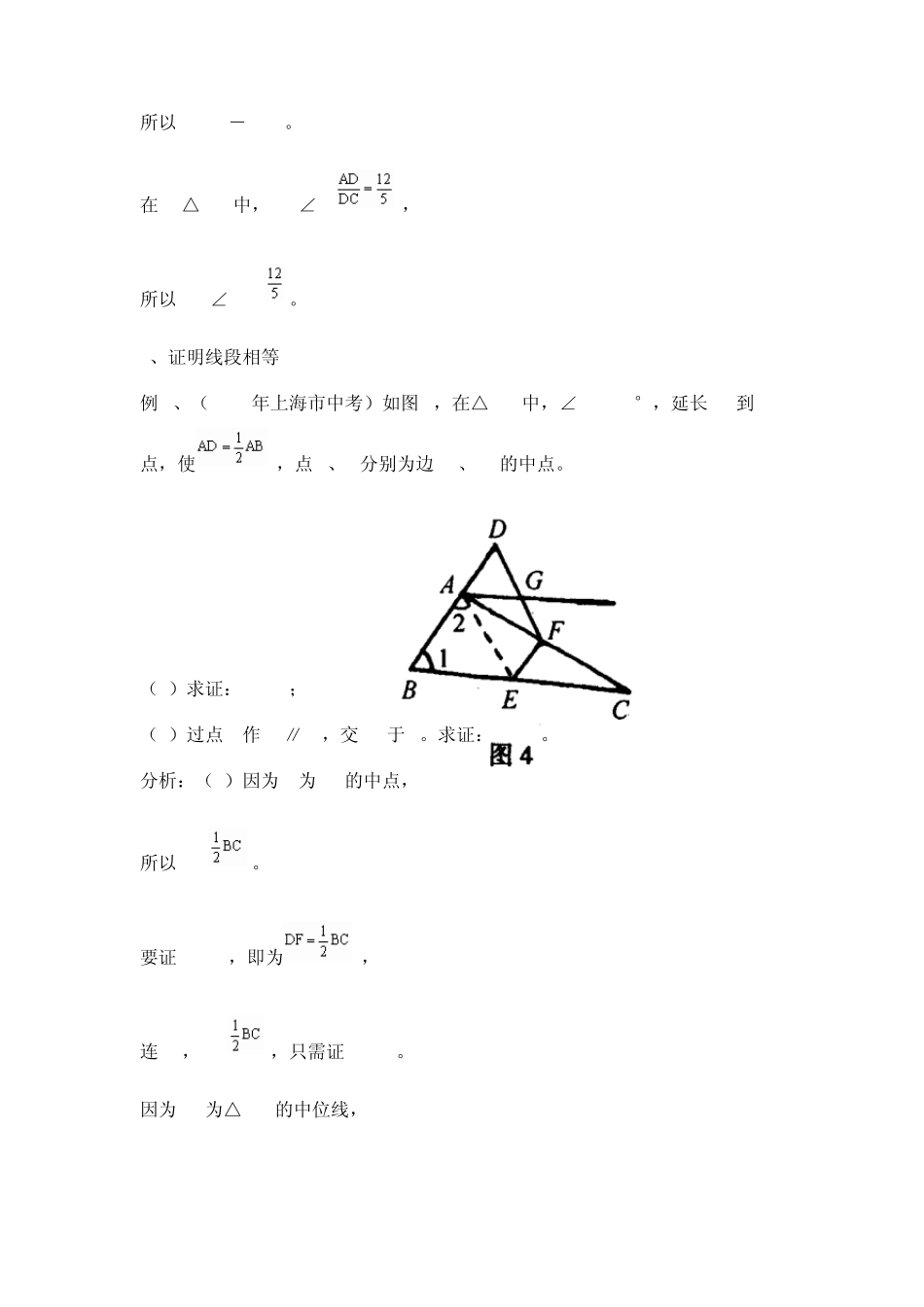
直角三角形斜边上中线性质的应用 蔡志武 张玉平 直角三角形斜边上中线的性质是直角三角形的一个重要性质,同时也是常考的知识点.它为证明线段相等、角相等、线段的倍分等问题提供了很好的思路和理论依据。但在初中数学教材中它却是以矩形性质(矩形的对角线相等)的推论形式出现的,因而很容易造成学生忽视这一性质的应用.从实际教学的反馈来看确有很多学生应用它解决问题有困难.下面谈谈直角三角形斜边上中线的性质及应用.仅供参考. 一、直角三角形斜边上中线的性质 1、性质:直角三角形斜边上的中线等于斜边的一半.如图1,在Rt△BAC中,∠BAC=,D为BC的中点,则。 2、性质的拓展:如图1:因为D为BC中点, 所以, 所以AD=BD=DC=, 所以∠1=∠2,∠3=∠4, 因此∠ADB=2∠3=2∠4, ∠ADC=2∠1=2∠2。 因而可得如下几个结论:①直角三角形斜边上的中线将直角三角形分成两个等腰三角形;②分成的两个等腰三角形的腰相等,两个顶角互补、底角互余,并且其中一个等腰三角形的顶角等于另一个等腰三角形底角的2倍. 二、性质的应用 1、求值 例1、(2004年江苏省苏州市中考)如图2,CD是Rt△ABC斜边AB上的中线,若CD=4,则AB= . 解析:由性质可知:CD, 所以AB=2CD=8. 例2、(2006年上海市中考)已知:如图3,在△ABC中,AD是BC边上的高,E为AC边上的中点,BC=14,AD=12, 。求的值。 解析:由性质拓展可知:∠EDC=∠C。要求tan∠EDC的值,可转化为求tan∠C的值。 在Rt△ADB中,, 所以AB=15。 由勾股定理得: , 所以DC=BC-BD=5。 在Rt△ADC中,tan∠C=, 所以tan∠EDC=。 2、证明线段相等 例3、(2004年上海市中考)如图4,在△ABC中,∠BAC=90°,延长 BA到 D点,使,点 E、F分别为边 BC、AC的中点。 (1)求证:DF=BE; (2)过点 A作 AG∥BC,交 DF于 G。求证:AG=DG。 分析:(1)因为 E为 BC的中点, 所以BE= 。 要证DF=BE,即为, 连 AE,AE= ,只需证DF=AE。 因为 EF为△ABC的中位线, 所以EF,而AD= , 所以 。 故四边形AEFD为平行四边形。 所以DF=AE,从而DF=BE这一命题得证。 (2)由性质拓展可知:∠1=∠2。 由(1)得AE∥DF,所以∠2=∠D。 因为AG∥BC,所以∠1=∠DAG, 因此∠D=∠DAG,所以DG=AG。 3、证明角相等及角的倍分关系 例4、已知,如图5,在△ABC中,∠BAC>90°,BD、CE分别为AC、AB上的高,F为BC的中点,求证:∠FED=∠FDE。 分析:因为BD、CE分别为AC...