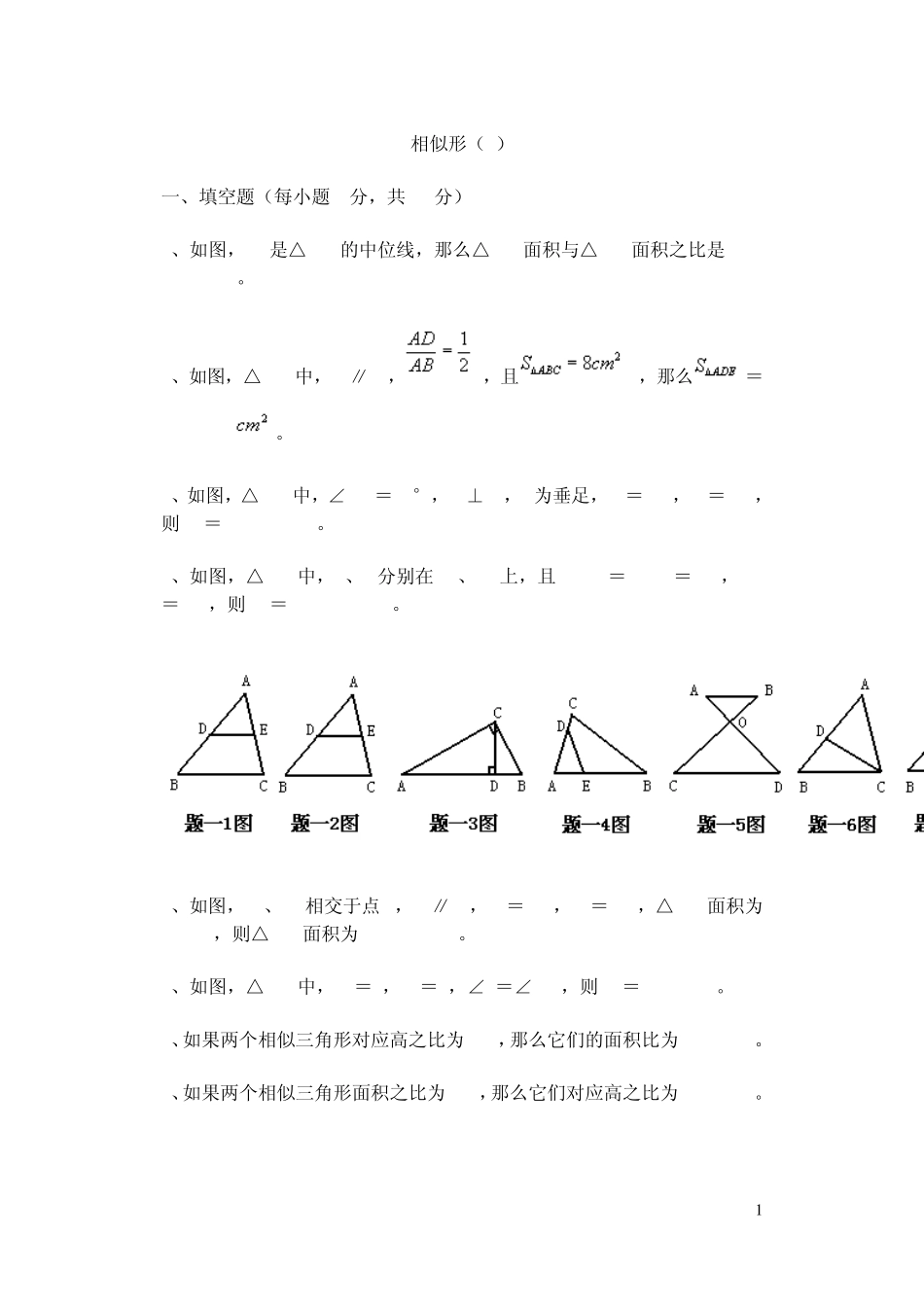
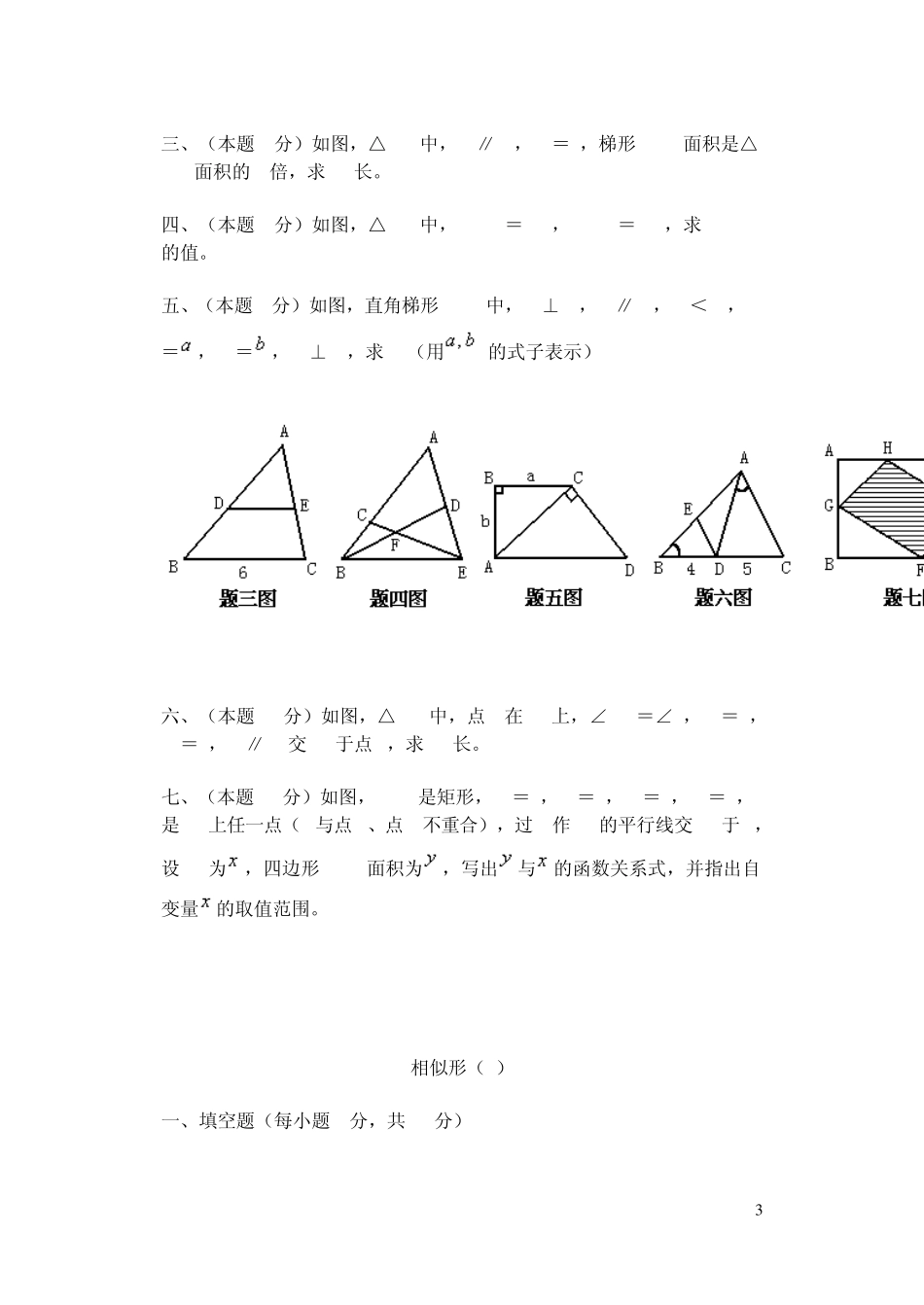
1 相似形(1) 一、填空题(每小题4分,共40分) 1、如图,DE是△ABC的中位线,那么△ADE面积与△ABC面积之比是________。 2、如图,△ABC中,DE∥BC,,且,那么=________。 3、如图,△ABC中,∠ACB=90°,CD⊥AB,D为垂足,AD=8cm,DB=2cm,则 CD=________cm。 4、如图,△ABC中,D、E分别在 AC、AB上,且AD:AB=AE:AC=1:2,BC=5cm,则 DE=________ cm。 5、如图,AD、BC相交于点 O,AB∥CD,OB=2cm,OC=4cm,△AOB面积为4.5cm2,则△DOC面积为________cm2。 6、如图,△ABC中,AB=7,AD=4,∠B=∠ACD,则 AC=________。 7、如果两个相似三角形对应高之比为 4:5,那么它们的面积比为________。 8、如果两个相似三角形面积之比为 1:9,那么它们对应高之比为________。 2 9、两个相似三角形周长之比为2:3,面积之差为10cm2,则它们的面积之和为________cm2。 10、如图,△ABC中,DE∥BC,AD:DB=2:3,则=________。 二、选择题(每小题 4分,共 16分) 1、两个相似三角形对应边之比是 1:5,那么它们的周长比是( )。 (A);(B)1:25;(C)1:5;(D)。 2、如果两个相似三角形的相似比为1:4,那么它们的面积比为( )。 (A)1:16;(B)1:8;(C)1:4;(D)1:2。 3、如图,锐角三角形ABC的高 CD和高 BE相交于 O,则与△DOB相似的三角形个数是( )。 (A)1;(B)2;(C)3;(D)4。 4、如图,梯形ABCD,AD∥BC,AC和BD相交于 O点,=1:9,则=( )。 (A)1:9;(B)1:81;(C)3:1;(D)l:3。 3 三、(本题8分)如图,△ABC中,DE∥BC,BC=6,梯形DBCE面积是△ADE面积的2倍,求DE长。 四、(本题8分)如图,△ABE中,AD:DB=5:2,AC:CE=4:3,求BF:FC的值。 五、(本题8分)如图,直角梯形ABCD中,AB⊥BC,BC∥AD,BC<AD,BC=,AB=,AC⊥CD,求AD(用的式子表示) 六、(本题10分)如图,△ABC中,点D在BC上,∠DAC=∠B,BD=4,DC=5,DE∥AC交 AB于点E,求DE长。 七、(本题10分)如图,ABCD是矩形,AH=2,HD=4,DE=2,EC=1,F是BC上任一点(F与点B、点C不重合),过 F作 EH的平行线交 AB于 G,设 BF为,四边形HGFE面积为,写出与的函数关系式,并指出自变量的取值范围。 相似形(2) 一、填空题(每小题4分,共 40分) 4 1、已知:,且,则=________。 2、在一张比例尺为1:5000的地图上,某校到果园的图距为8cm,那么学校到果园的实际距离为_...