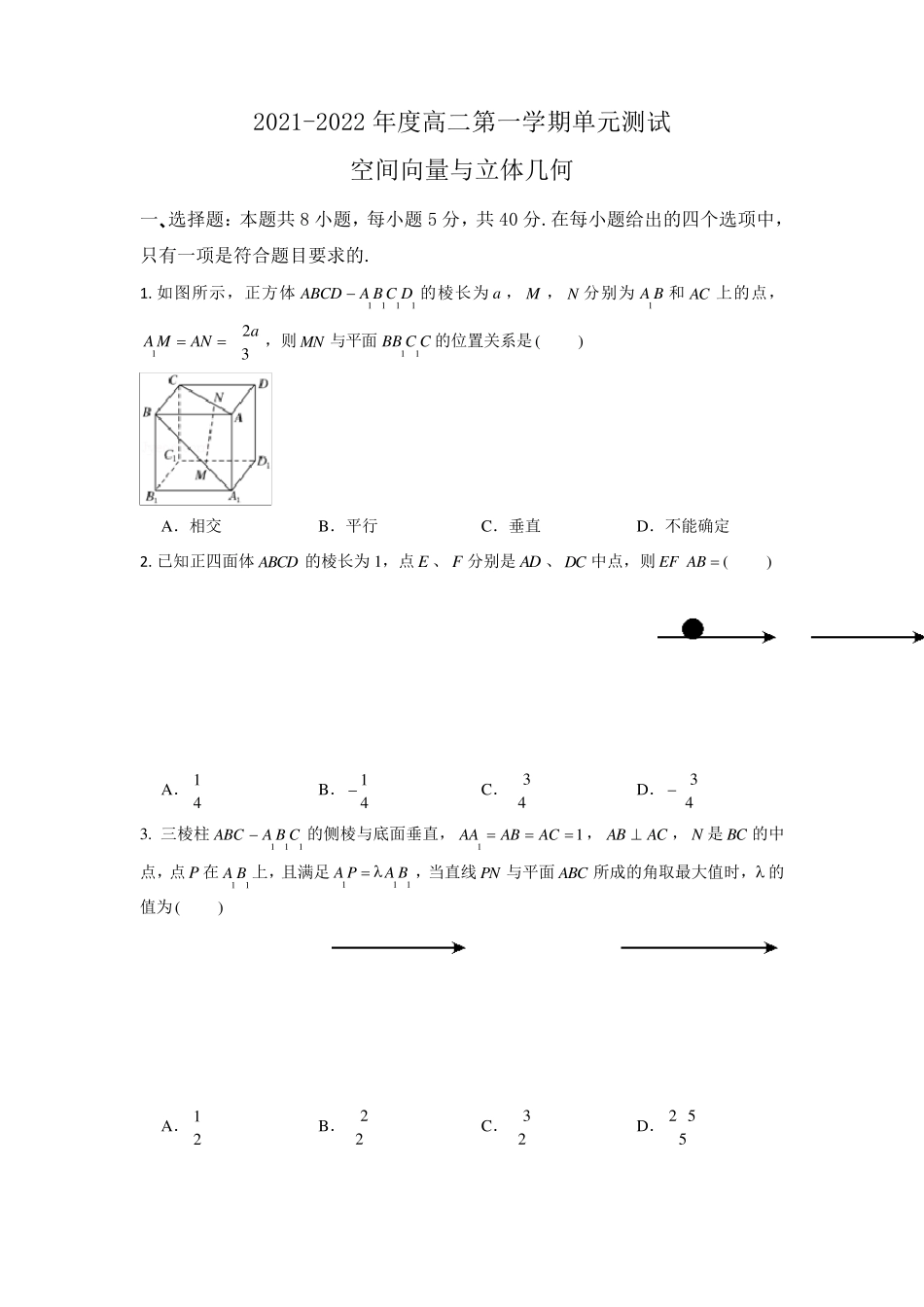
2021-2022 年度高二第一学期单元测试 空间向量与立体几何 一、选择题:本题共8 小题,每小题5 分,共40 分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 如图所示,正方体1111ABCDA B C D的棱长为a ,M ,N 分别为1A B 和AC 上的点,123aA MAN,则MN 与平面11BB C C 的位置关系是( ) A.相交 B.平行 C.垂直 D.不能确定 2. 已知正四面体ABCD 的棱长为1,点E 、 F 分别是AD 、 DC 中点,则(EF AB ) A.14 B.14 C.34 D.34 3. 三棱柱111ABCA B C的侧棱与底面垂直,11AAABAC ,ABAC,N 是BC 的中点,点P 在11A B 上,且满足111A PA B,当直线 PN 与平面ABC 所成的角取最大值时,的值为( ) A.12 B.22 C.32 D.2 55 4. 如图,在长方体1111ABCDA B C D中, 2AB ,3BC ,16AA ,则异面直线1AB 与1BC 所成角的大小为( ) A.60 B.45 C.30 D.15 5. 如图,60 的二面角的棱上有A ,B 两点,直线AC ,BD 分别在这个二面角的两个半平面内,且都垂直于AB .已知4AB ,6AC ,8BD ,则CD 的长为( ) A.17 B.7 C.2 17 D.9 6. 在棱长为2 的正方体1111ABCDA B C D中,E ,F 分别为11A D ,11D C 的中点,则过B ,E ,F 三点的平面截该正方体,所得截面的周长为( ) A.5 2 B.6 2 C.22 13 D.24 13 7. 在长方体1111ABCDA B C D中, 2AB ,11BCAA ,点M 为1AB 的中点,点P 为对角线1AC 上的动点,点Q 为底面ABCD 上的动点(点P 、Q 可以重合),则MPPQ的最小值为( ) A.22 B.32 C.34 D.1 8. 把正方形 ABCD 沿对角线BD 折成直二面角,对于下列结论: ① ACBD;② ADC是正三角形;③ AB 与CD 成60 角;④ AB 与平面BCD 成60 角. 则其中正确结论的个数是( ) A.1 个 B.2 个 C.3 个 D.4 个 三、填空题:本题共4 小题,每小题5 分,共20 分. 1 3 . 如图,动点P 在正方体1111ABCDA B C D的对角线1BD 上,过点P 作垂直于平面11BB D D的直线,与正方体表面相交于M ,N 两点,设BPx,MNy,则函数( )yf x的图象大致是 ② .(在横线上填上正确的序号,多选少选都不得分) 1 4 .如图,矩形ABCD 中,2ABAD,E 为边AB 的中点,将ADE沿直线DE ...