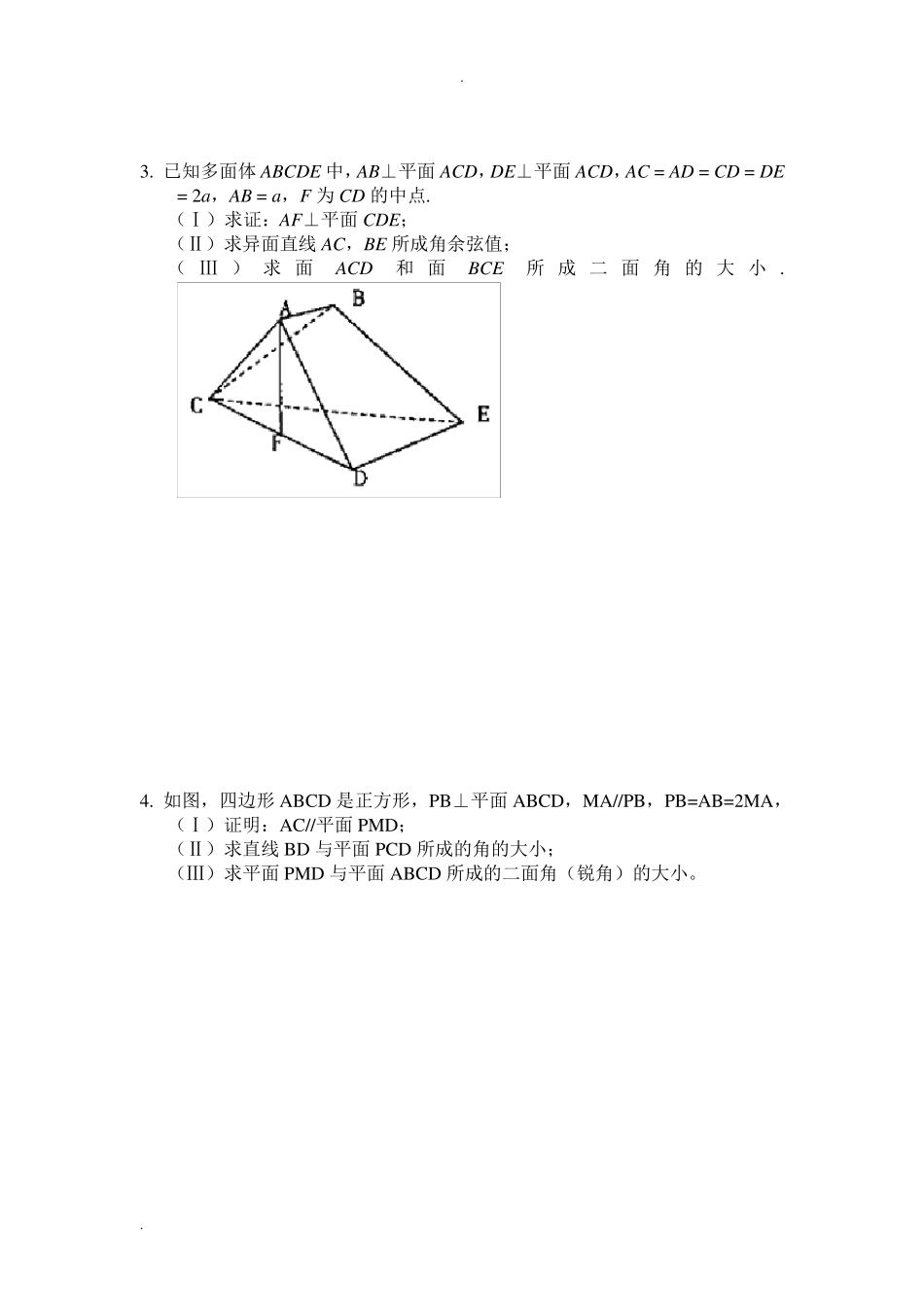
. . 空间立体几何建系设点专题 引入空间向量坐标运算,使解立体几何问题避免了传统方法进行繁琐的空间分析,只需建立空间直角坐标系进行向量运算,而如何建立恰当的坐标系,成为用向量解题的关键步骤之一.所谓“建立适当的坐标系”,一般应使尽量多的点在数轴上或便于计算 1、如图所示,四棱锥 P—ABCD 中,AB AD,CD AD,PA 底面 ABCD,PA=AD=CD=2AB=2,M 为PC 的中点。 (1)求证:BM∥平面 PAD; (2)在侧面 PAD 内找一点N,使MN 平面 PBD; (3)求直线 PC 与平面 PBD 所成角的正弦。 . . 3. 已知多面体ABCDE 中,AB⊥平面ACD,DE⊥平面ACD,AC = AD = CD = DE = 2a,AB = a,F 为CD 的中点. (Ⅰ)求证:AF⊥平面CDE; (Ⅱ)求异面直线 AC,BE 所成角余弦值; (Ⅲ ) 求 面ACD和 面BCE所 成 二 面角 的大 小 . 4. 如图,四边形 ABCD 是正方形,PB⊥平面ABCD,MA//PB,PB=AB=2MA, (Ⅰ)证明:AC//平面PMD; (Ⅱ)求直线 BD 与平面PCD 所成的角的大小; (Ⅲ)求平面PMD 与平面ABCD 所成的二面角(锐角)的大小。 . . 5. 已知斜三棱柱111ABCA B C,90BCA,2ACBC,1A 在底面ABC 上的射影恰为AC 的中点D ,又知11BAAC。 (I)求证:1AC 平面1A BC ; (II)求1CC 到平面1A AB 的距离; (III)求二面角1AA BC的大小。 6. (湖南卷理科第18 题)已知两个正四棱锥P-ABCD 与 Q-ABCD 的高都为2,AB=4. (1)证明:PQ⊥平面ABCD; (2)求异面直线 AQ 与PB 所成的角; (3)求点P 到平面QAD 的距离. . . 7. (全国卷Ⅱ理科第 19 题)在直三棱柱111ABCA B C中,AB=BC,D、E 分别为11BBAC,的中点. (1)证明:ED 为异面直线1BB 与1AC 的公垂线; (2)设12AAACAB,求二面角11AADC的大小. 8. 如图,平面 PAC 平面 ABC ,ABC是以 AC 为斜边的等腰直角三角形,,,E F O 分别为PA , PB ,AC 的中点,16AC ,10PAPC. (I)设 G 是OC 的中点,证明:/ /FG平面 BOE ; (II)证明:在 ABO内存在一点 M ,使 FM 平面 BOE ,并求点 M 到OA ,OB 的距离. . . 9. 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD 为等腰梯形,AB//CD,AB=4, BC=CD=2, AA1=2, E、E1、F 分别是棱AD、AA1、AB 的中点。 (1) 证明:直...