立体几何专题训练

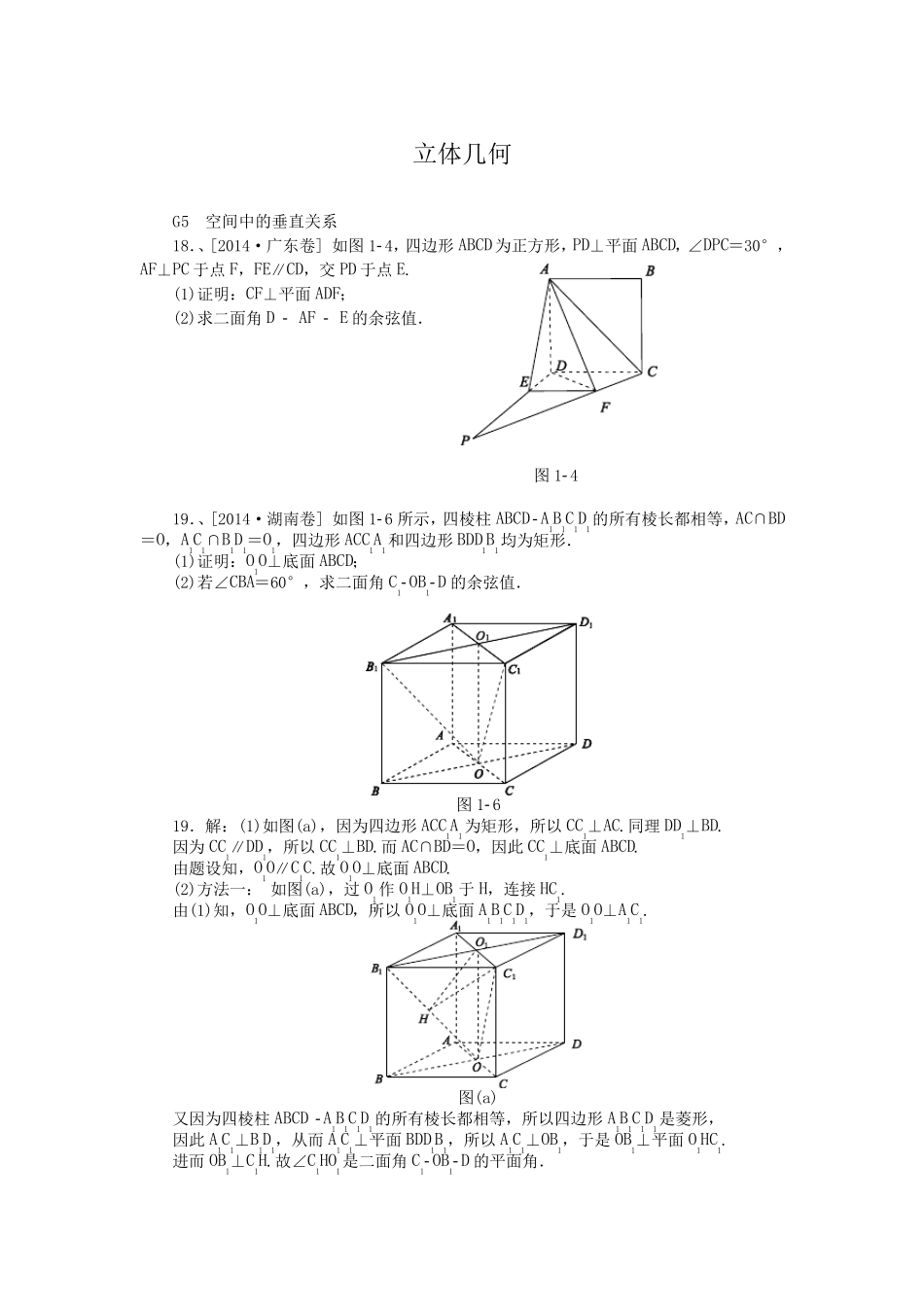
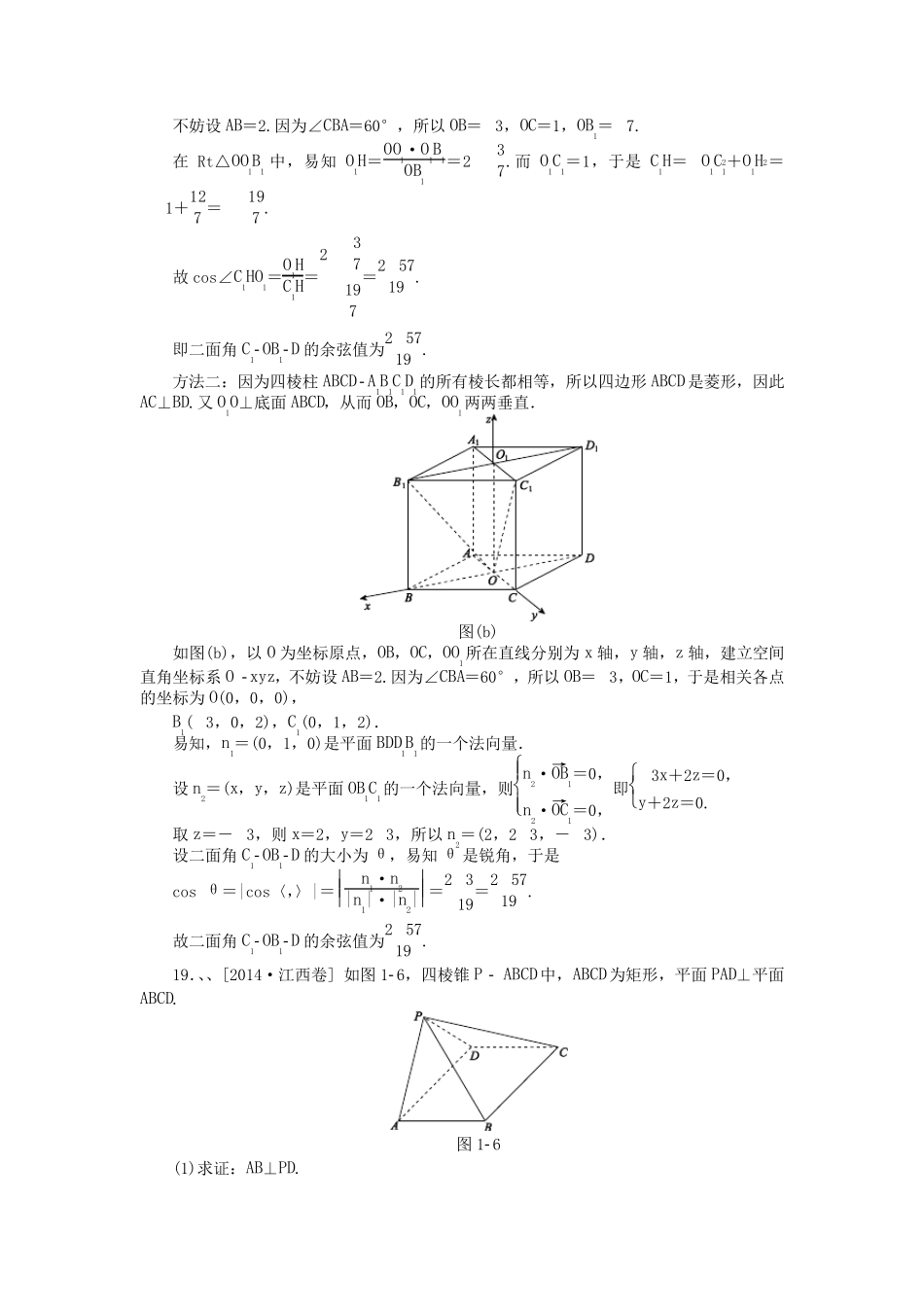
立体几何 G5 空间中的垂直关系 18．、[2014·广东卷] 如图1­4，四边形ABCD为正方形，PD⊥平面ABCD，∠DPC＝30°，AF⊥PC 于点 F，FE∥CD，交 PD 于点 E. (1)证明：CF⊥平面ADF； (2)求二面角 D ­ AF ­ E 的余弦值． 图1­4 19．、[2014·湖南卷] 如图1­6 所示，四棱柱 ABCD ­A1B1C1D1的所有棱长都相等，AC∩BD＝O，A1C1∩B1D1＝O1，四边形ACC1A1和四边形BDD1B1均为矩形． (1)证明：O1O⊥底面ABCD； (2)若∠CBA＝60°，求二面角 C1­OB1­D 的余弦值． 图1­6 19．解：(1)如图(a)，因为四边形ACC1A1为矩形，所以 CC1⊥AC.同理 DD1⊥BD. 因为CC1∥DD1，所以 CC1⊥BD.而 AC∩BD＝O，因此 CC1⊥底面ABCD. 由题设知，O1O∥C1C.故 O1O⊥底面ABCD. (2)方法一： 如图(a)，过 O1作 O1H⊥OB1于 H，连接 HC1. 由(1)知，O1O⊥底面ABCD，所以 O1O⊥底面A1B1C1D1，于是 O1O⊥A1C1. 图(a) 又因为四棱柱 ABCD ­A1B1C1D1的所有棱长都相等，所以四边形A1B1C1D1是菱形， 因此 A1C1⊥B1D1，从而 A1C1⊥平面BDD1B1，所以 A1C1⊥OB1，于是 OB1⊥平面O1HC1. 进而 OB1⊥C1H.故∠C1HO1是二面角 C1­OB1­D 的平面角． 不妨设AB＝2.因为∠CBA＝60°，所以OB＝3，OC＝1，OB1＝7. 在Rt△OO1B1 中，易知O1H＝OO1·O1B1OB1＝237.而O1C1＝1，于是C1H＝O1C21＋O1H2＝1＋127 ＝197 . 故cos∠C1HO1＝O1HC1H＝237197＝2 5719 . 即二面角C1­OB1­D 的 余 弦 值 为2 5719 . 方 法 二： 因为四 棱 柱 ABCD ­A1B1C1D1的 所有 棱 长 都 相 等 ，所以四 边 形 ABCD是菱 形 ，因此AC⊥ BD.又 O1O⊥ 底 面ABCD，从 而OB，OC，OO1两 两 垂 直 ． 图 (b) 如 图 (b)，以O 为坐 标 原 点 ，OB，OC，OO1所在直 线 分 别 为x 轴 ，y 轴 ，z 轴 ，建 立 空 间直 角坐 标 系 O ­xyz，不妨设AB＝2.因为∠CBA＝60°，所以OB＝3，OC＝1，于是相 关 各 点的 坐 标 为O(0，0，0)， B1( 3，0，2)，C1(0，1，2)． 易知，n1＝(0，1，0)是平 面BDD1B1的 一 个 法 向 量 ． 设n2＝(x，y，z)是平 面OB1C1的 一 个 法 向 量 ，则n2·OB→1＝0，n2·OC→1＝0，即 3x＋2z＝0，y＋2z＝0. 取 z＝－3，则 x＝2，y＝2 3，所以n2＝(2，2 3，－3)． 设二面角C1­OB1­D 的 大 小 为θ ，易知θ 是锐 角，于是 cos...