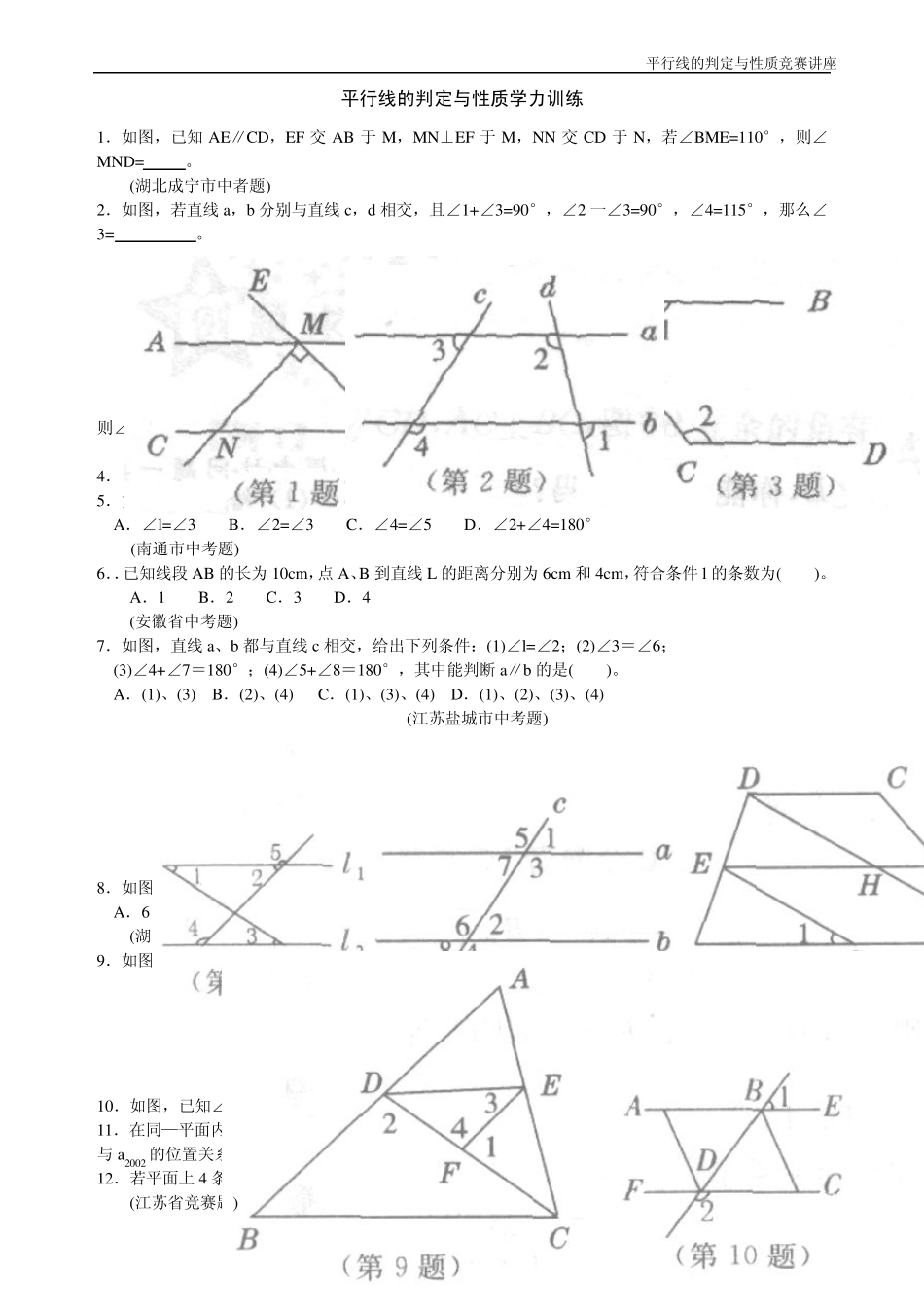
平行线的判定与性质竞赛讲座 Pag e 1 o f 6 第二十二讲 平行线的判定与性质 在同一平面内,不相交的两条直线叫做平行线。 角是平面几何图形中最活跃的元素,前面我们已学习过特殊角、数量关系角、等角的知识。当两条直线相交或分别与第三条直线相交,就产生对顶角、同位角、内错角、同旁内角等位置关系角,进一步丰富了角的知识,它们在角的计算与证明中有广泛的应用。 与平行线相关的问题一般都是平行线的判定与性质的综合运用,主要体现在如下两个方面: 1、由角定角 已知角的关系→(判定)两直线平行→(性质)确定其他角的关系。 2、由线定线 已知两直线平行→(性质)角的关系→(判定)确定其他两直线平行。 例题 【例 1】如图,AB∥CD,AC⊥BC,图中与∠CAB 互余的角有 个。 (安徽省中考题) 思路点拨:充分运用对顶角、平行线性质等与角相关的知识,借助互余的概念判断。 注:平面几何的研究除了运用计算方法外,更多的是要依靠图形的观察(直觉能力),运用演绎推理的方法去完成,往往需要通过观察、实验操作进而猜想结论(性质),或由预设结论去猜想条件,再运用演绎推理方法加以证明。 在学习完相交线、平行线内容后,平面几何的学习就由实验几何阶段进入论证几何阶段,顺利跨越推理论证阶段,需注意以下几点:(1)过好语言关;(2)学会识图;(3)善于分析。 【例 2】 如图,平行直线 AB、CD 与相交直线 EF、GH 相交,图中的同旁内角共有( ) 。 A、4 对 B、8 对 C、12 对 D、16 对 ( “希望杯”邀请赛试题) 思路点拨:每一个“三线八角”基本图形都有两对同旁内角,从对原图形进行分解人手。 【例 3】如图,已知∠B=25°,∠BCD=45°,∠CDE=30°,∠E=10°求征:AB∥EF。 思路点拨:解本例的困难在于图形中没有“三线八角”,考虑创造条件,在图中添置“三线八角”或作出与 AB 或 CD 平行的直线。 【例 4】 如图,在Δ ABC 中,CE⊥AB 于E,DF⊥AB 于F,AC∥ED,CE 是∠ACB 的平分线.求证:∠EDF=∠BDF。(天津市竞赛题) 思路点拨:综合运用角平分线、垂直的定义、平行线的判定与性质等知识,因图形复杂,故需恰当分解图形。 【例 5】 探究: (1)如图 a,若 AB∥CD,则∠B+∠D=∠E,你能说明为什么吗? (2)反之,若∠B+∠D=∠E,直线 AB 与 CD 有什么位置关系?请证明; (3)若将点 E 移至图 b 所示位置,此时∠B、∠D、∠E 之间有什么关系?请证明; (4)...