第4章多自由度系统的振动题解

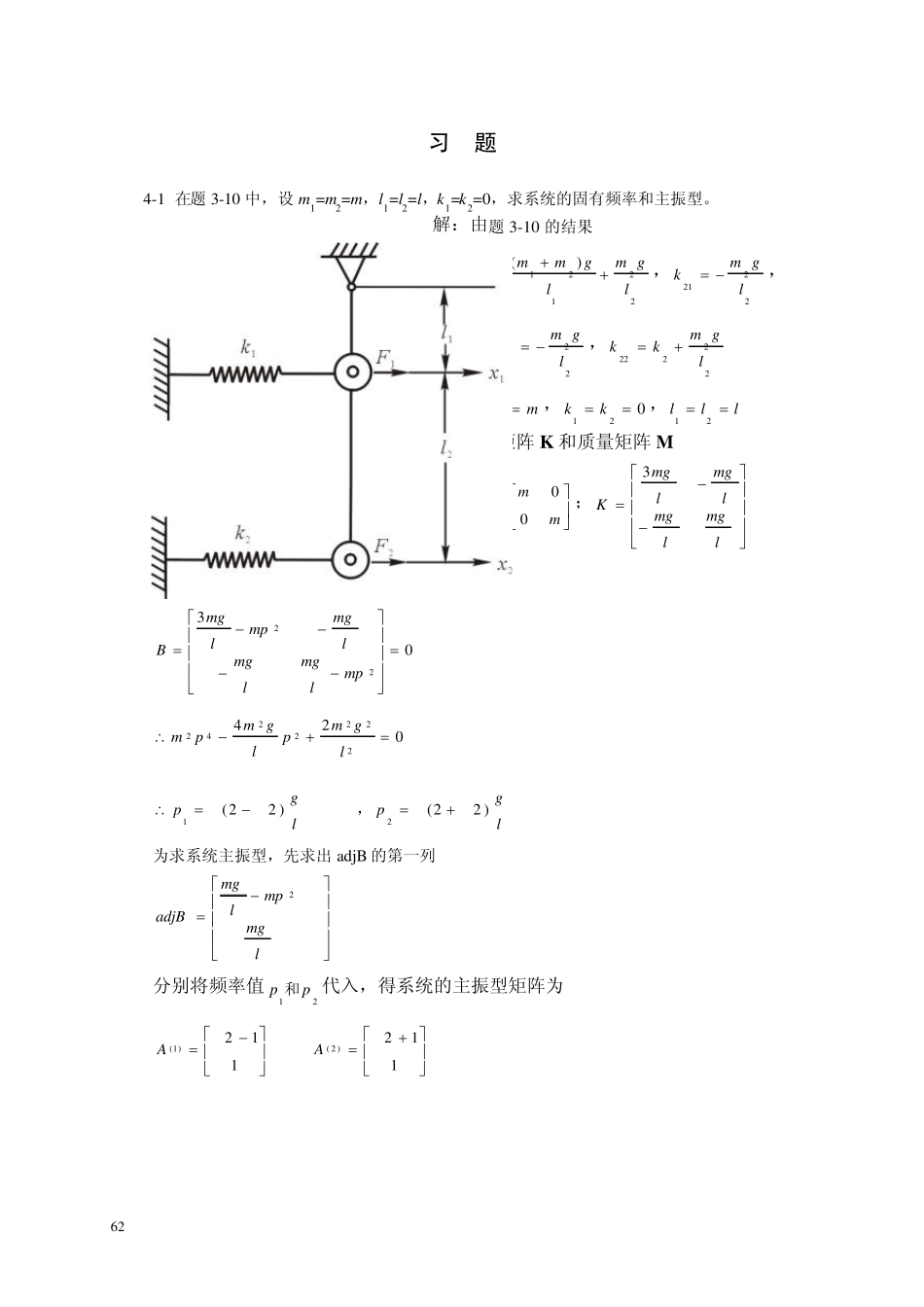
62 习 题 4-1 在题3-10 中，设m1=m2=m，l1=l2=l，k1=k2=0，求系统的固有频率和主振型。 解：由题3-10 的结果 22121111)(lgmlgmmkk，2221lgmk，2212lgmk，22222lgmkk 代入mmm21，021 kk， lll21 可求出刚度矩阵 K 和质量矩阵 M mmM00；lmglmglmglmgK3 由频02MpK，得 0322mplmglmglmgmplmgB 0242222242lgmplgmpm lgp)22(1 ，lgp)22(2 为求系统主振型，先求出 adjB 的第一列 lmgmplmgadjB2 分别将频率值21pp 和代入，得系统的主振型矩阵为 112)1(A 112)2(A 题4-1 图 63 4-2 题4-2 图所示的均匀刚性杆质量为m1，求系统的频率方程。 解：设杆的转角 和物块位移 x 为广义坐标。利用刚度影响系数法求刚度矩阵 k。 设0,1x，画出受力图，并施加物体力偶与力2111 , kk，由平衡条件得到， 222111akbkk， akk221 设1,0x，画出受力图，并施加物体力偶与力2212 , kk，由平衡条件得到， 12kak2， akk222  得作用力方程为 0000312222221221xakakakakbkxmam 由频率方程02MKp，得 031222222212221pmakakakpamakbk 4-3 题4-3 图所示的系统中，两根长度为l 的均匀刚性杆的质量为m1 及 m2，求系统的刚度矩阵和柔度矩阵，并求出当 m1=m2=m 和k1=k2=k 时系统的固有频率。 解：如图取21, 为广义坐标，分别画受力图。由动量矩定理得到， llkllkI43434343211111 224343434322211122llkllkllkI 整理得到， 016916922112111lklkI 题4-3 图 题4-2 图 6 4 0)41 69(1 692222112122lklklkI 则刚度矩阵和柔度矩阵分别得， 2212121212411 691 691 691 69klklklklklK，2222222122144491 641lklklklklkadj KKK 系统的质量矩阵为2221214 87003100lmlmIIM 由频率方程02MKp，并代入已知条件得， 04 871 61 31 691 69311 6922222222pmlklklklpmlkl 整...