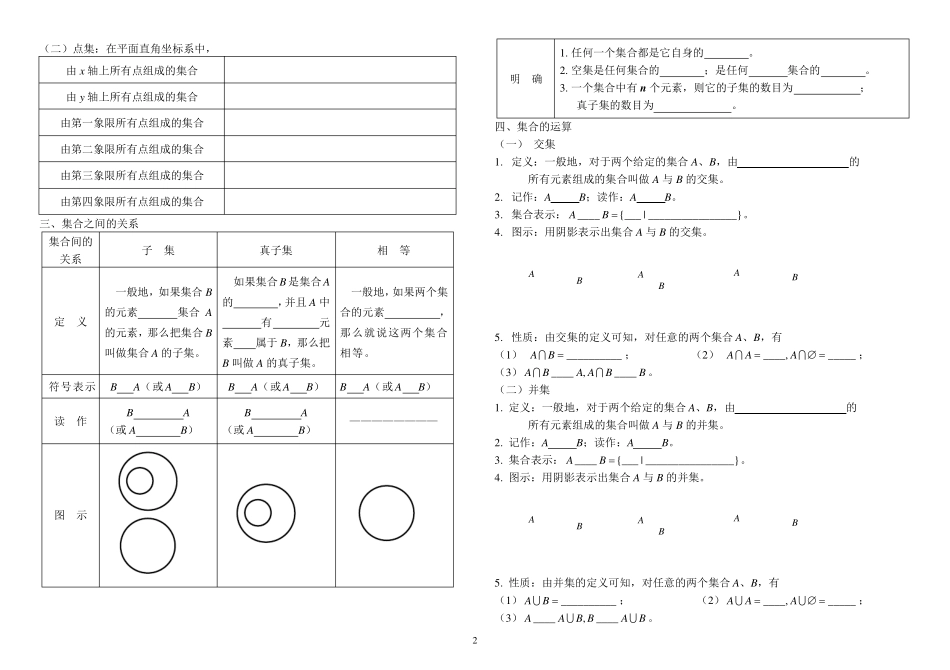
1 第一章 集合与充要条件 一、集合的概念 (一)概念 1 . 集合的概念:将某些 的对象看成一个 就构成一个集合,简称为 。 一般用 表示集合。 组成集合的对象叫做这个集合的 。 一般用 表示集合中的元素。 2 . 集合与元素之间关系: 如果 a是集合A 的元素,就说 a A,记作 ; 如果 a不是集合A 的元素,就说 a A,记作 。 3 . 集合的分类: 含有 的集合叫做有限集; 含有 的集合叫做无限集; 的集合叫做空集,记作 。 (二) 常用的数集:数集就是由 组成的集合。 1 . 自然数集:所有 组成的集合叫做自然数集,记作 ; 2 . 正整数集:所有 组成的集合叫做正整数集,记作 ; 3 . 整数集:所有 组成的集合叫做整数集,记作 ; 4 . 有理数集:所有 组成的集合叫做有理数集,记作 ; 5 . 实数集:所有 组成的集合叫做实数集,记作 。 (三) 应知应会: 1 . 自然数:由 和 构成的实数。 2 . 整数:由 和 构成的实数。 偶数: 被 2 整除的数叫做偶数; 奇数: 被 2 整除的数叫做奇数。 3 . 分数:把 平均分成若干份,表示这样的 或 的数叫做分数。分数中间的 叫做分数线。分数线 的数叫做分母,表示把一个物体 ;分数线 的数叫做分子,表示 。 4 . 有理数: 和 统称有理数。 5 . 无理数: 的小数叫做无理数。 6 . 实数: 和 统称实数。 二、集合的表示法 表 示 法 列 举 法 描 述 法 定 义 将集合中的元素 表示集合的方法。 利用元素的 来表示集合的方法。 具体方法 1 . 将集合中的元素 ; 2 . 用 分隔; 3 . 用 括为一个整体。 1 . 在 中画一条 ; 2 . 左侧写上集合的 , 并标出元素的 ;(如果上下文中能够明显看出集合中的元素为实数,可以不标出元素的取值范围。) 3 . 右侧写出元素所具有的 。 【注】在使用描述法表示某些集合时,可以用 来叙述集合的 ,再用 括起来。 优 点 明确、直接看到集合中的元素。 清晰地反映出元素的特征性质。 不 足 能表示的集合有限。 抽象,不能直接看出元素。 适用类型 一般用来表示有限集。 一般用来表示无限集。 【几个常用集合的表示方法】 (一)数集: 集 合 列举法 描述法 偶数集合 正偶数集合 负 偶数集合 奇数集合 正奇数集合 负 奇数集合 2 (二)点集:在平面直角坐标系中, 由x轴上所有点组成的集合 由...