自动控制原理C作业(第二章)答案

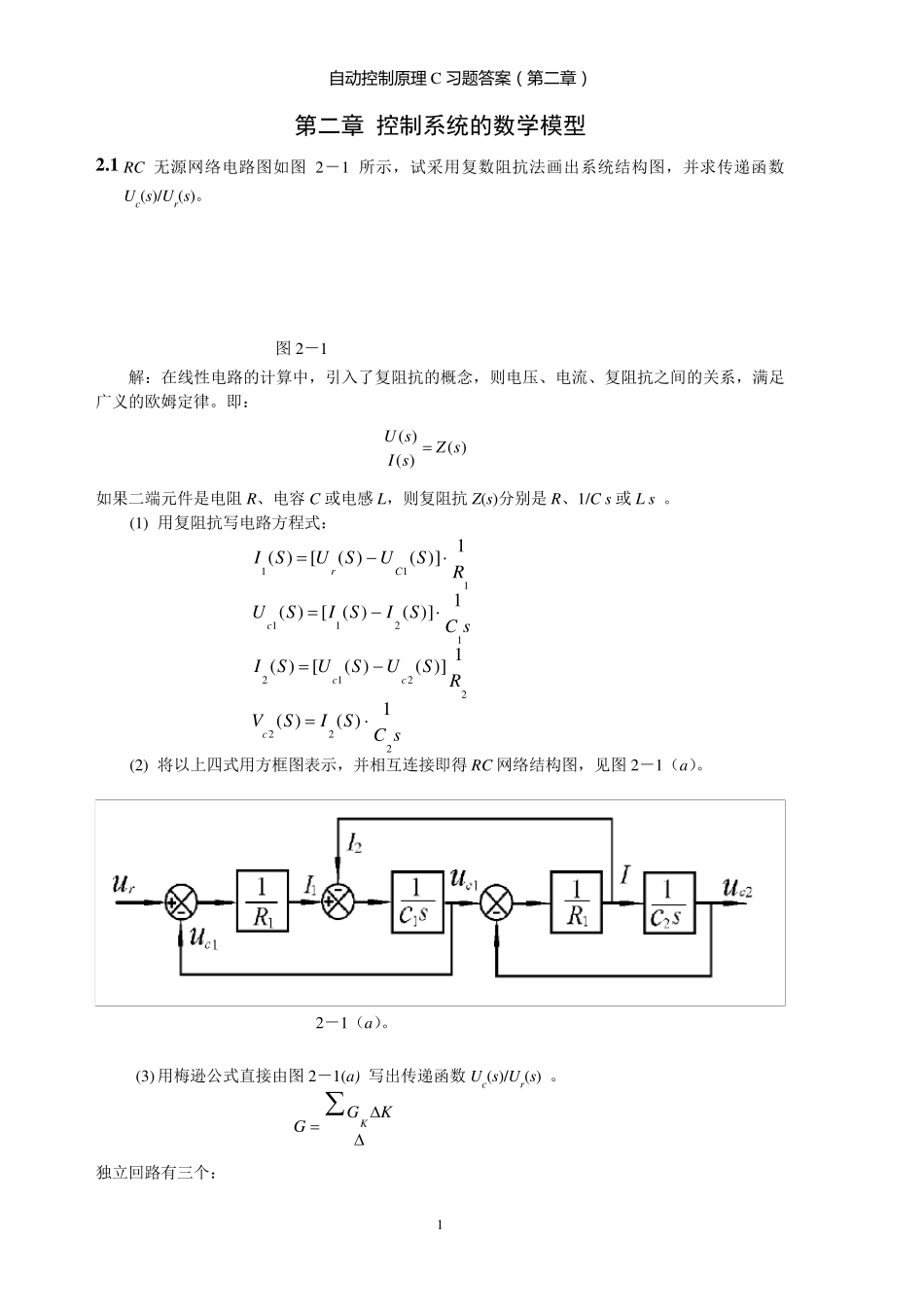
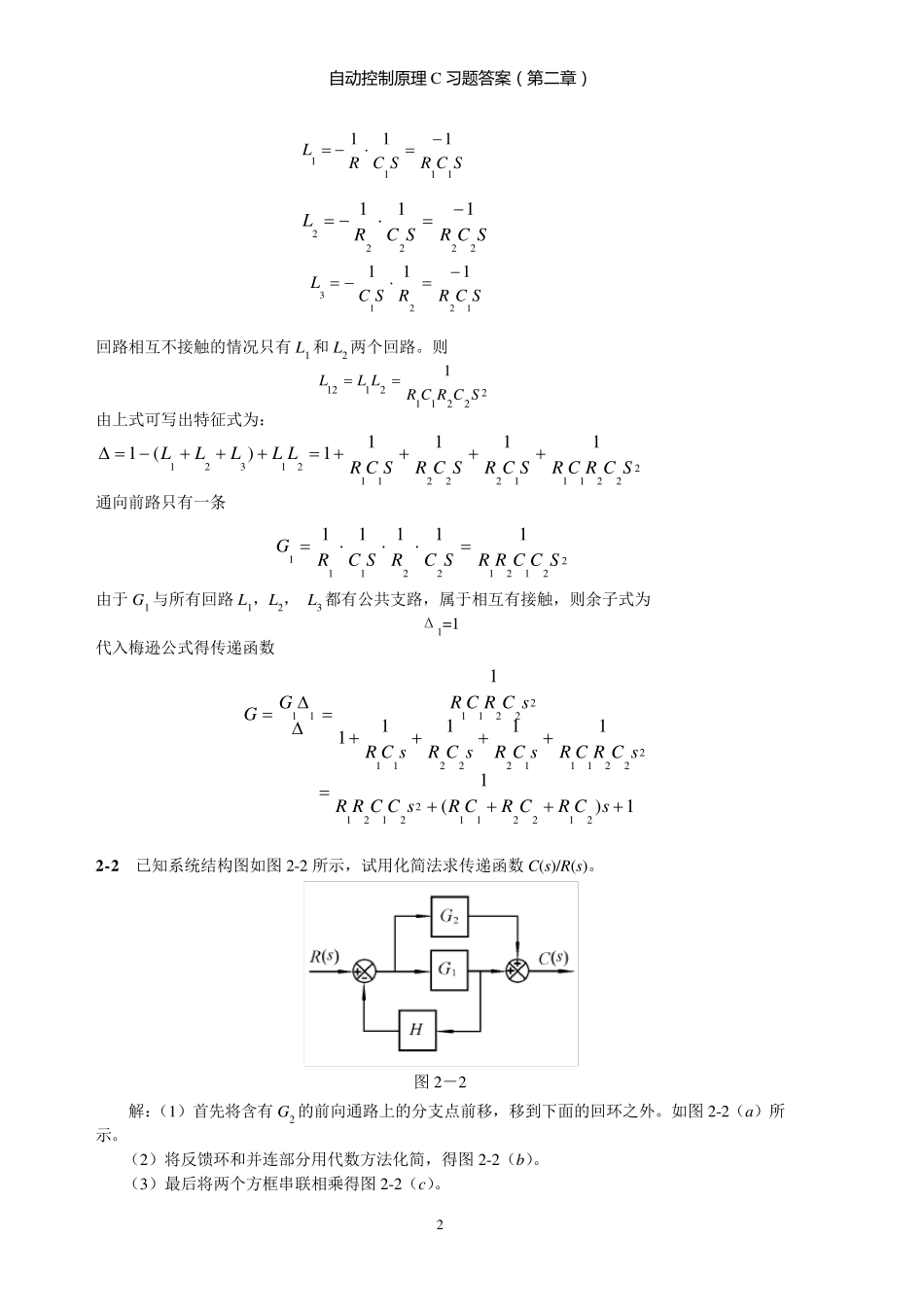
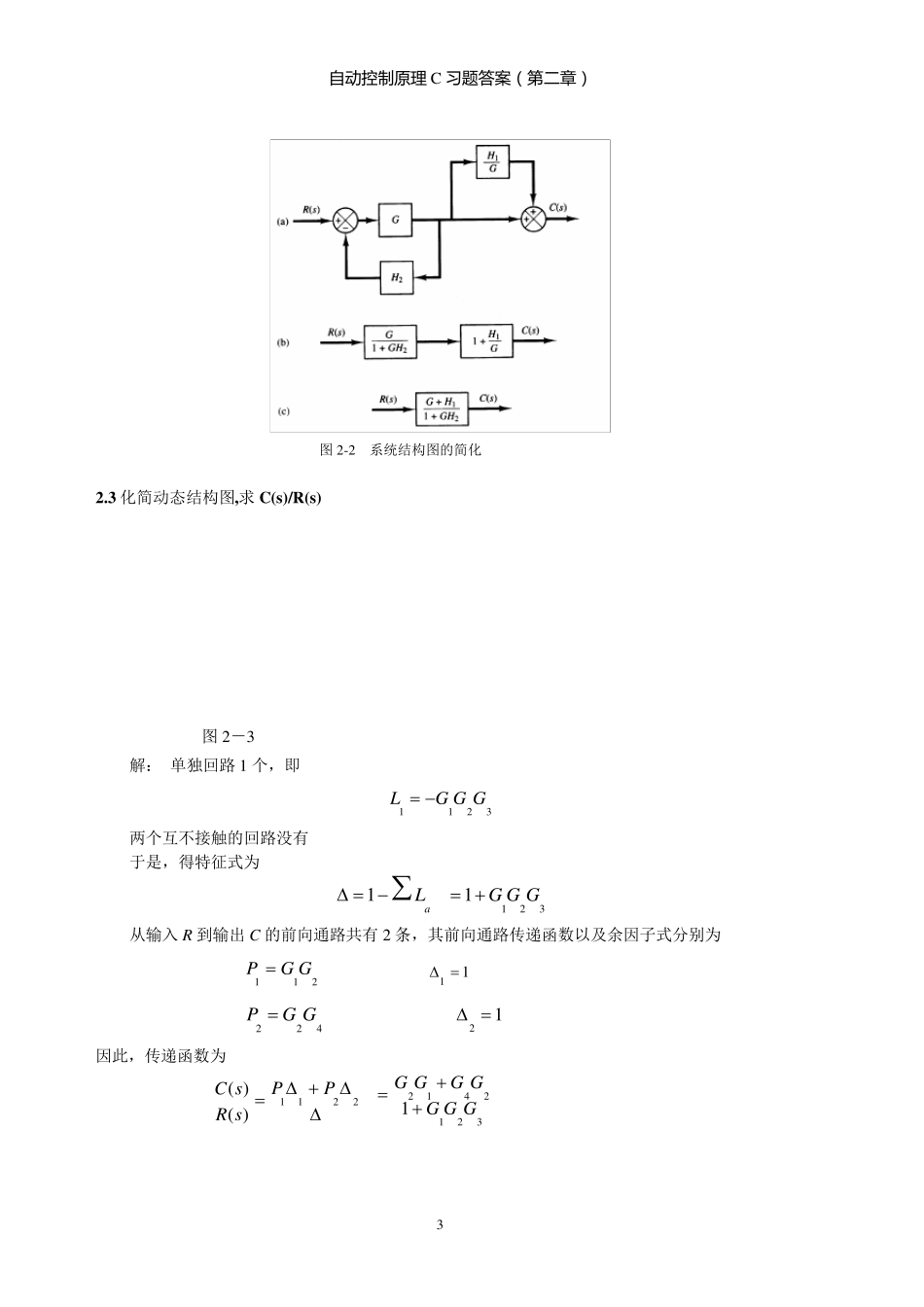
自 动 控 制 原 理 C 习题答案（第二章） 1 第二章 控制系统的数学模型 2 .1 RC 无源网络电路图如图2－1 所示，试采用复数阻抗法画出系统结构图，并求传递函数Uc(s)/Ur(s)。 图2－1 解：在线性电路的计算中，引入了复阻抗的概念，则电压、电流、复阻抗之间的关系，满足广义的欧姆定律。即： )()()(sZsIsU 如果二端元件是电阻R、电容 C 或电感 L，则复阻抗Z(s)分别是 R、1/C s 或 L s 。 (1) 用复阻抗写电路方程式： sCSISVRSUSUSIsCSISISURSUSUSIccccCr222221212111111)()(1)]()([)(1)]()([)(1)]()([)( (2) 将以上四式用方框图表示，并相互连接即得 RC 网络结构图，见图2－1（a）。 2－1（a）。 (3) 用梅逊公式直接由图2－1(a) 写出传递函数Uc(s)/Ur(s) 。  KGGK 独立回路有三个： 自 动 控 制 原 理 C 习题答案（第二章） 2 SCRSCRL1111111 SCRSCRL22222111 回路相互不接触的情况只有L1 和L2 两个回路。则 2221121121SCRCRLLL 由上式可写出特征式为： 222111222112132111111)(1SCRCRSCRSCRSCRLLLLL 通向前路只有一条 221212211111111SCCRRSCRSCRG 由于G1 与所有回路L1，L2， L3 都有公共支路，属于相互有接触，则余子式为 Δ1=1 代入梅逊公式得传递函数 1)(1 11111121221122121222111222112221111sCRCRCRsCCRRsCRCRsCRsCRsCRsCRCRGG 2 -2 已知系统结构图如图 2-2 所示，试用化简法求传递函数 C(s)/R(s)。 图 2－2 解：（1）首先将含有G2 的前向通路上的分支点前移，移到下面的回环之外。如图 2-2（a）所示。 （2）将反馈环和并连部分用代数方法化简，得图 2-2（b）。 （3）最后将两个方框串联相乘得图 2-2（c）。 SCRRSCL12213111自 动 控 制 原 理 C 习题答案（第二章） 3 图2-2 系统结构图的简化 2.3 化简动态结构图,求C(s)/R(s) 图2－3 解： 单独回路1 个，即 3211GGGL 两个互不接触的回路没有 于是，得特征式为 3211 1GGGLa 从输入 R 到输出 C 的前向通路共有 2 条，其前向通路传递函数以及余因子式分别为 211GGP  11  422GGP  12  因此，传递函数为 2211)()(PPsRsC 32124121GGGGGGG自 动 控 制 原 理 C 习题答案（第二章...