自动控制原理超前滞后控制

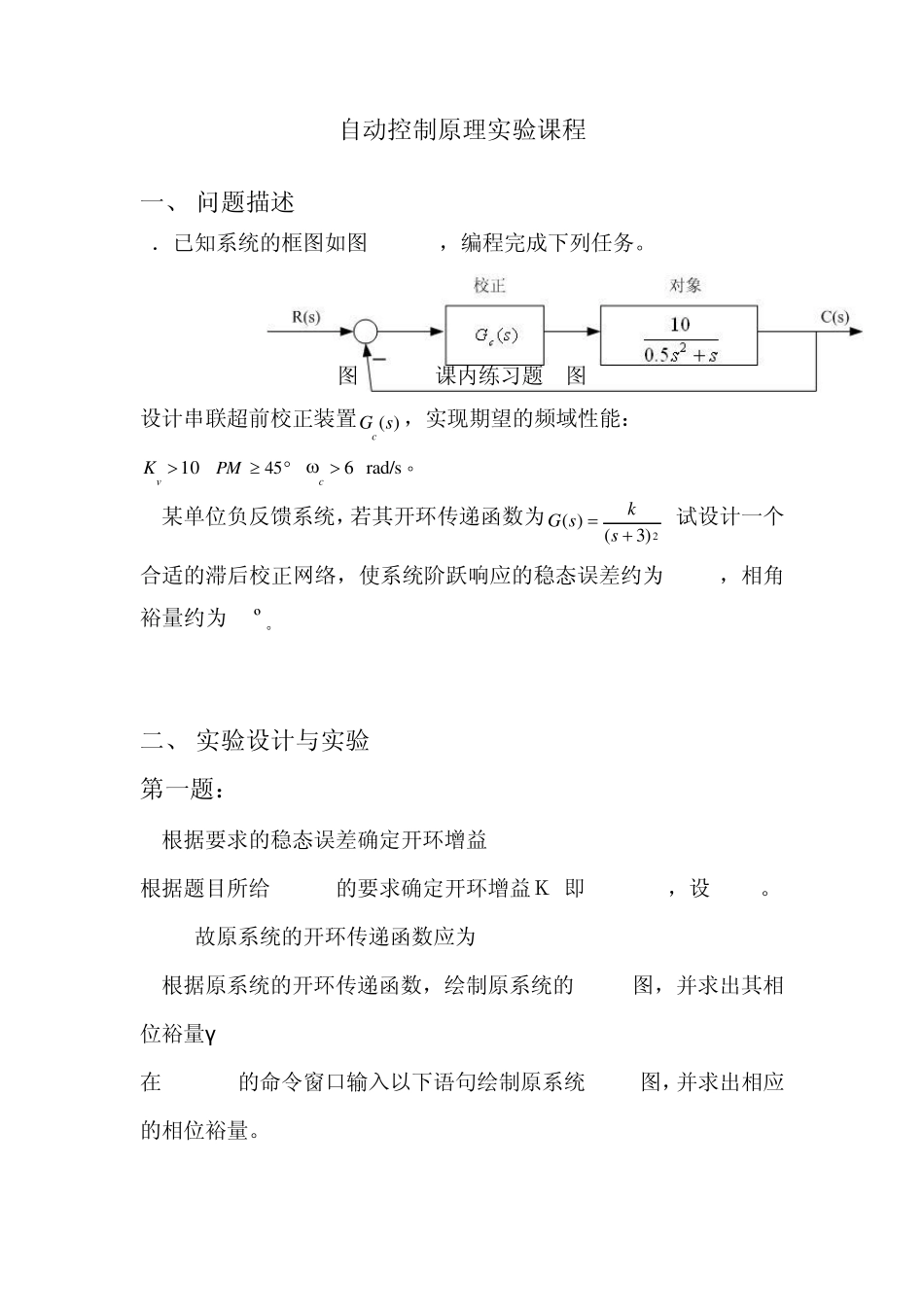
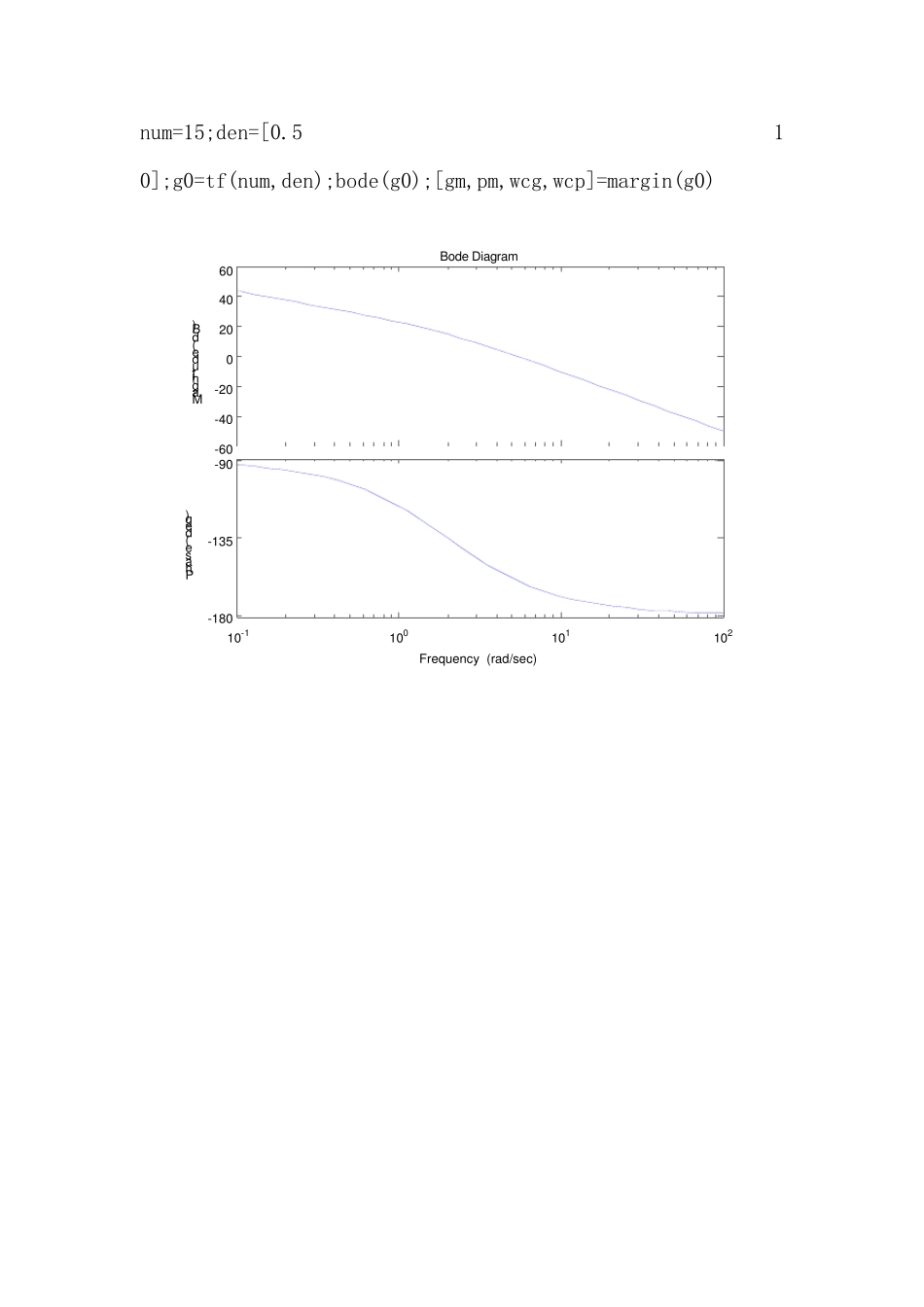
自动控制原理实验课程 一、 问题描述 1．已知系统的框图如图2-5-30，编程完成下列任务。 图2-5-30课内练习题4图 设计串联超前校正装置)(sGc，实现期望的频域性能： 10vK, 45PM,rad/s 6c。 2.某单位负反馈系统，若其开环传递函数为2)3()( sksG,试设计一个合适的滞后校正网络，使系统阶跃响应的稳态误差约为0.04，相角裕量约为45º。 二 、 实验设计与 实验 第 一题： 1.根 据 要 求 的稳态误差确 定 开环增 益 K 根 据 题目 所 给 Kv>10的要 求 确 定 开环增 益 Ｋ ,即 Kv=K>10，设K=15。 故 原系统的开环传递函数应为 2.根 据 原系统的开环传递函数，绘 制原系统的Bode图，并 求 出 其相位裕量γ 在 MATLAB的命 令 窗 口 输 入 以 下语 句 绘 制原系统Bode图，并 求 出 相应的相位裕量。 num=15;den=[0.5 1 0];g0=tf(num,den);bode(g0);[gm,pm,wcg,wcp]=margin(g0) -60-40-200204060Magnitude (dB)10-1100101102-180-135-90Phase (deg)Bode DiagramFrequency (rad/sec) 由运行的结果可知：原系统的相位裕量pm=20.6824，不满足系统性能指标要求。 3.设置补偿角，求原系统相频特性曲线上的最大超前相角 设置的补偿角取值范围为10°-15°，假设补偿角为12°，题目要求的相位裕量为45°。在 MATLAB的命令窗口输入以下语句可求出原系统相频特性曲线上的最大超前相角： r=45;e=12;dpm=r-pm+e;phi=dpm*pi/180; 由运行结果可知：原系统相频特性曲线上的最大超前相角dpm为36.3176。 4.计算超前校正网络参数 a 在 MATLAB的命令窗口输入以下语句可求出参数 a： a=(1+sin(phi))/(1-sin(phi)) 由运行的结果可知：超前校正网络参数 a为3.9051。 5.求超前校正装置在ω ｍ处的对数幅频值 mm=-10*log10(a) 在原系统幅频特性曲线上找到对应的频率ω ｍ [mu,pu,w]=bode(num,den); mu_db=20*log10(mu); wm=spline(mu_db,w,mm) 由运行结果可知：前校正装置在ω ｍ处的对数幅频值mm为-5.9163，在原系统幅频特性曲线上找到对应的频率ω ｍ为7.5708rad/s，满足题目要求wm>6rad/s。 6.根据ω ｍ=ω c ′，求超前校正网络参数T。 wc=wm; T=1/(wc*sqrt(a)) 由运行的结果可知：超前校正网络参数T为0.0668。 7.校验性能指标是否已达到要求 nk=[a*T 1]; dk=[T 1]; gc=tf(nk,dk) g=g0*gc [gm1,pm1,wcg1,wcp1]=margin(g) 由运行的结果可知：校正后...