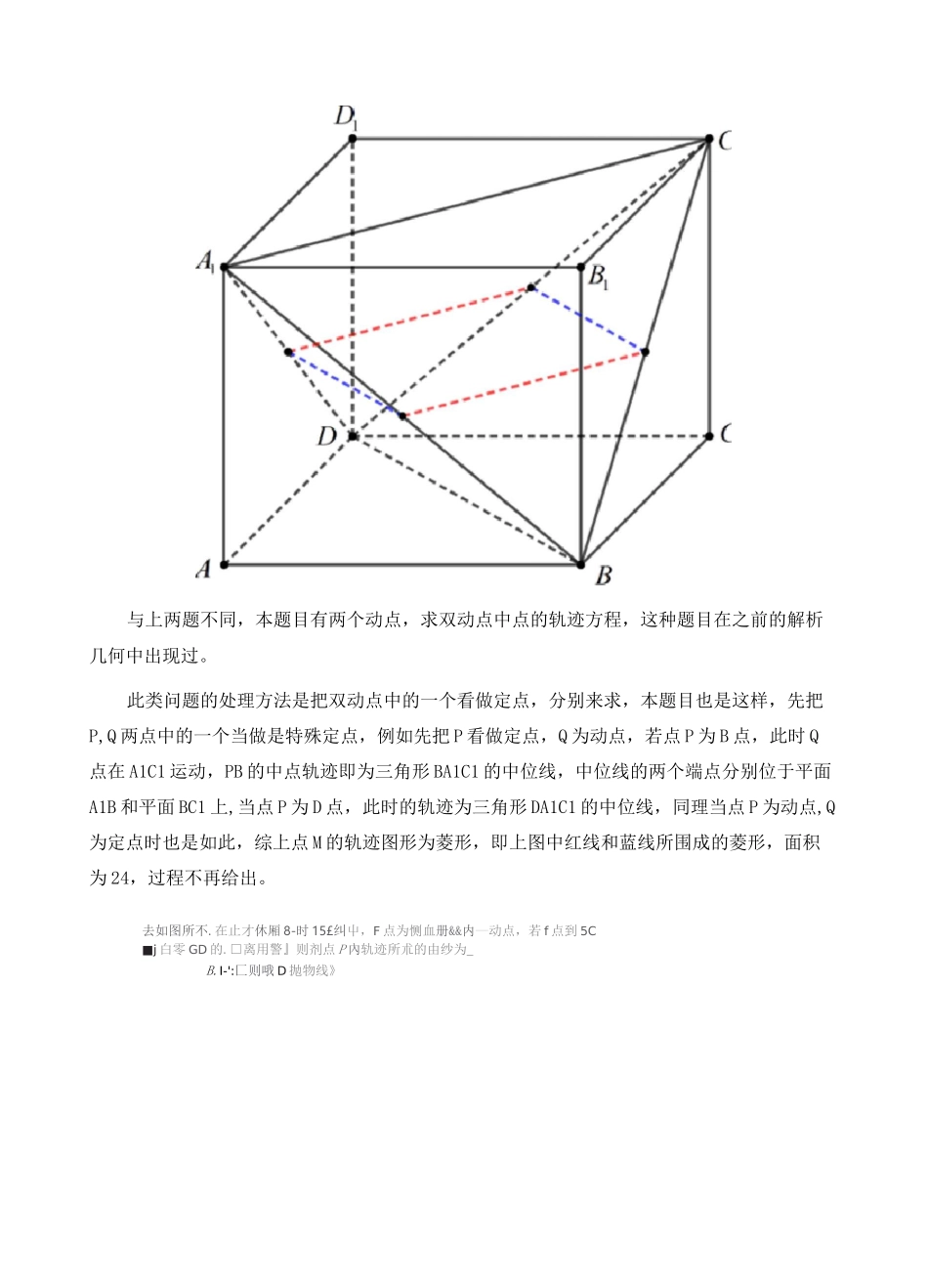
立体几何中的动点轨迹问题讲解这类问题在高考中并不常见,或者说在高考中出现得并不明显,但在用空间向量求二面角时偶尔会遇到一种题目,即需要用到的点并不是一个确定的点,而是在一个面上的动点,且这个点还满足一些特定的值或平面几何关系,此时需要根据条件确定出动点所在的轨迹,在每年高考前的模拟题中也会遇到这种题目,若在选填中,则一般位于压轴或次压轴位置,求几何体中动点的轨迹或者与轨迹求值相关的问题,在解析几何中满足条件的动点都会有特定的轨迹,动点绝不是乱点,在几何体中依旧如此。这种题目做法和平面几何求轨迹方程类似,因为点在面内(非平面),所求的轨迹一般有四种,即线段型,平面型,二次曲线型,球型,这四种情况没有过于明显的界限,知道就好,下列题目中就不再分门别类的去叙述了。立体几何中与动点轨迹有关的题目归根到底还是对点线面关系的认知,其中更多涉及了平行和垂直的一些证明方法,在此类问题中要么很容易的看出动点符合什么样的轨迹(定义),要么通过计算(建系)求出具体的轨迹表达式,和解析几何中的轨迹问题并没有太大区别。解机 O 占作鑫旨上的從舔 CT.3 丄则丄毛更玖疋冷AM1OO'工壹 EQO 与训西辱 C 的交錢为隅」所以动点 P 的就益为世段但题目是在规则的正方体中,直线 OP 和 AM 为异面直线,两者成 90。的特殊角度,根据射影法求异面直线的夹角方法,我们只需确定出 OP 在底面上的投影位置即可。逻?为学旳立蜒见讨爲 DP 的夹空,疋为川 M 卡.DP 痊底面上投孝怕丸定,粘色分釈肖曲化 CZP-弓”匿禹甘殳.审,可埒:cosfl?=Casarcost^cos-sinsin*斫以 cos 口 cos 址=0:戏恙 cos 电=0.斫队 uffl?cr=0,因此花底面与.1A1 垂直 QP 的投弄海 OB 护站京 F 的瓠远勺竄段期:"’变式:已知正方体曲 CD-吗巧匚占中,点 PO:面 JJQ 及边界上运蔚,卫总保持肿丄码,;「;:"F 的轨迹为且螳段&CE 込 CC.5C-IJ:5JCL:|:JI:I.IIJ。痊接丑巧和 CT】屮.二:为线段亠与上题类似,需要找到一个与 BD1 垂直且包含 AP 的平面,根据三垂线定理可知 BD1 丄AC,BD1 丄 AB1,所以 BD1 丄平面 ACB1,平面 ACB1 与有侧面的交线为 B1C,所以点 P 的轨迹为线段B1C2.长占林一岱 CD-4 耳 q 码 I-血=£旦 7=6 也緘段皿”如\上各有-点巴 Q 在吃 l-.f•; 点 M,且 RM■二站£,则点 M 的轨.迹阁形的面积为"与上两题不同,本题目有两个动点,求双动点中...