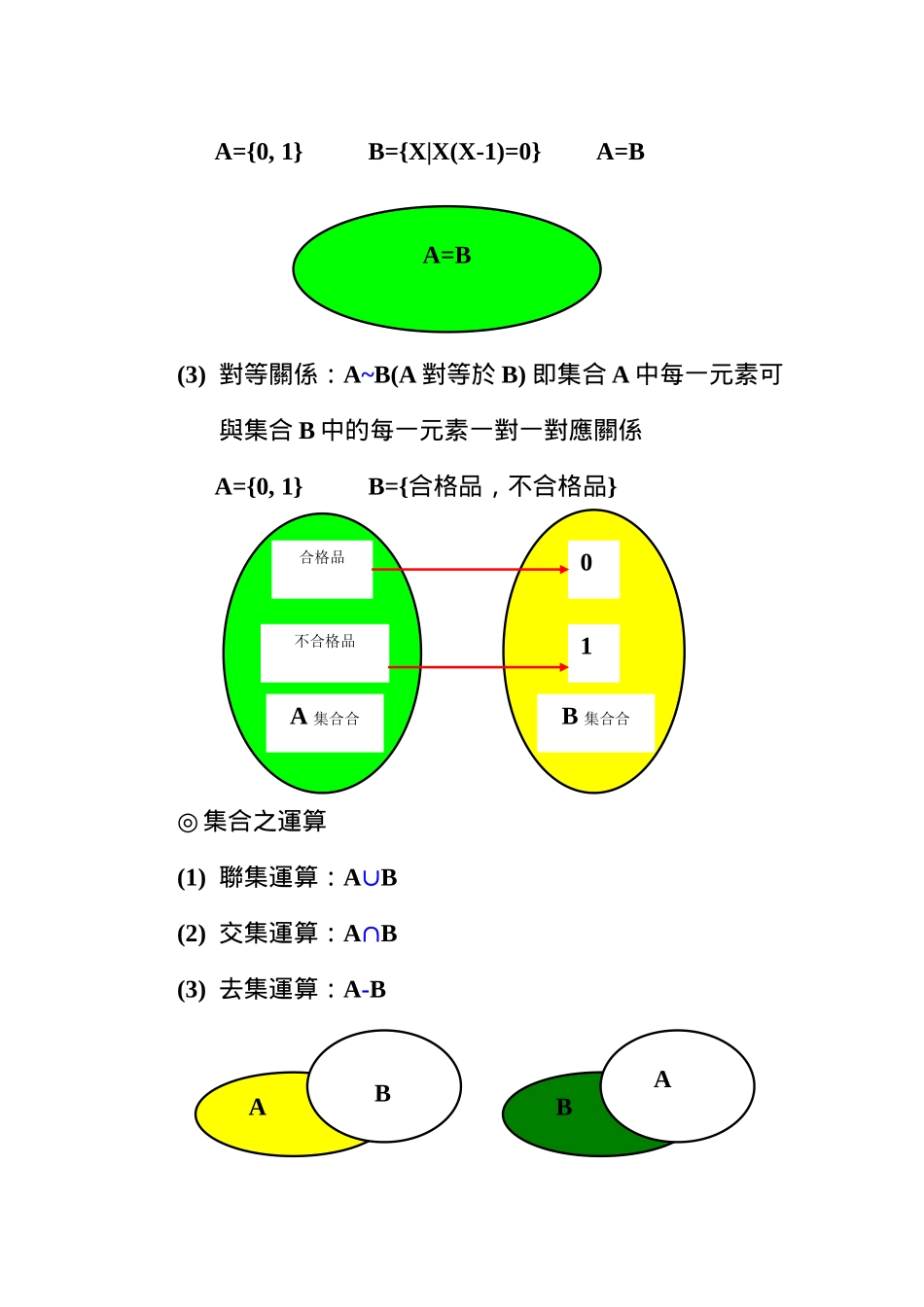
授 課 目 錄第一章 品質管理概說第二章 統計學概論第三章機率概論及機率分派 第四章 統計製程管制與管制圖第五章 計量值管制圖第六章 計數值管制圖第七章 製程能力分析第八章 允收抽樣的基本措施第九章 計數值抽樣計畫第十章 計量值抽樣計畫第十一章量具之再現度與再生度第十二章品質管理之新七大手法BA3.1 集合論◎ 集合論(Set Theory)機率論(Probability)群體分派◎ 集合是元素的聚合,而元素是集合的單位。A={1, 2, 3}1, 2, 3 為 A 集合的單位1A無元素的集合存在,稱之為空集合,記做{ }或 例 集合 B={X|X2+6X+5=0} 求 B={-1, -5}◎ 元素和集合的關係A={1, 2, 3} 1A ; 4A◎ 集合和集合的關係(1) 子集關係:AB(A 含於 B 或 B 包含 A)即 A 中任一元素均在 B 集合中可找到A={1, 2, 3}B={1, 2, 3, 4}AB(2) 等集關係:A=B(A 等於 B)即集合 A 與集合 B 中的元素完全相似 第三章 機率概論及機率分派A=B合格品不合格品A 集合合B 集合合10ABBAA={0, 1}B={X|X(X-1)=0}A=B(3) 對等關係:A~B(A 對等於 B) 即集合 A 中每一元素可與集合 B 中的每一元素一對一對應關係A={0, 1}B={合格品,不合格品}◎ 集合之運算(1) 聯集運算:AB(2) 交集運算:AB(3) 去集運算:A-BA’AAB(4) 結合律:ABC=(AB)C=A(BC)(5) 交換律:AB =BA(6) 分派律:A(BC)=(AB)(AC)(7) 餘集:設為全集,則-A 稱之為 A 之餘集,記作 A’,-A=A’若 A’A=A’A=(A’)’=A另 A-B= A B’(8) 分割:設為全集,集合 A、B 均含於,當滿足(a)AB=(b) AB=時,則稱為 A、B 為上的分割。(9) 餘集律:(AB)’=A’B’(AB)’=A’B’******************符號說明:X:隨機變數,P:機率,p:不合格率p(x):機率密度函數(離散型)f(x):機率密度函數(連續型)F(x):累積機率分派函數(連續型、離散型)E[X] = (期望值),V[X] = 2 (變異數) :母體平均值,2:母體變異數¯x :樣本平均值,S2:樣本變異數***********************3.2 機率的概念◎ 機率論是現代統計學的基礎。機率是為了衡量不確定結果,而建構出來的一種測度。其中基本的概念為:※機率空間(Probability Space):系統中,集合所有也许出現的事件而構成的一個抽象空間,一般以表达。有 時 亦 稱 樣 本 空 間 (Sample Space...