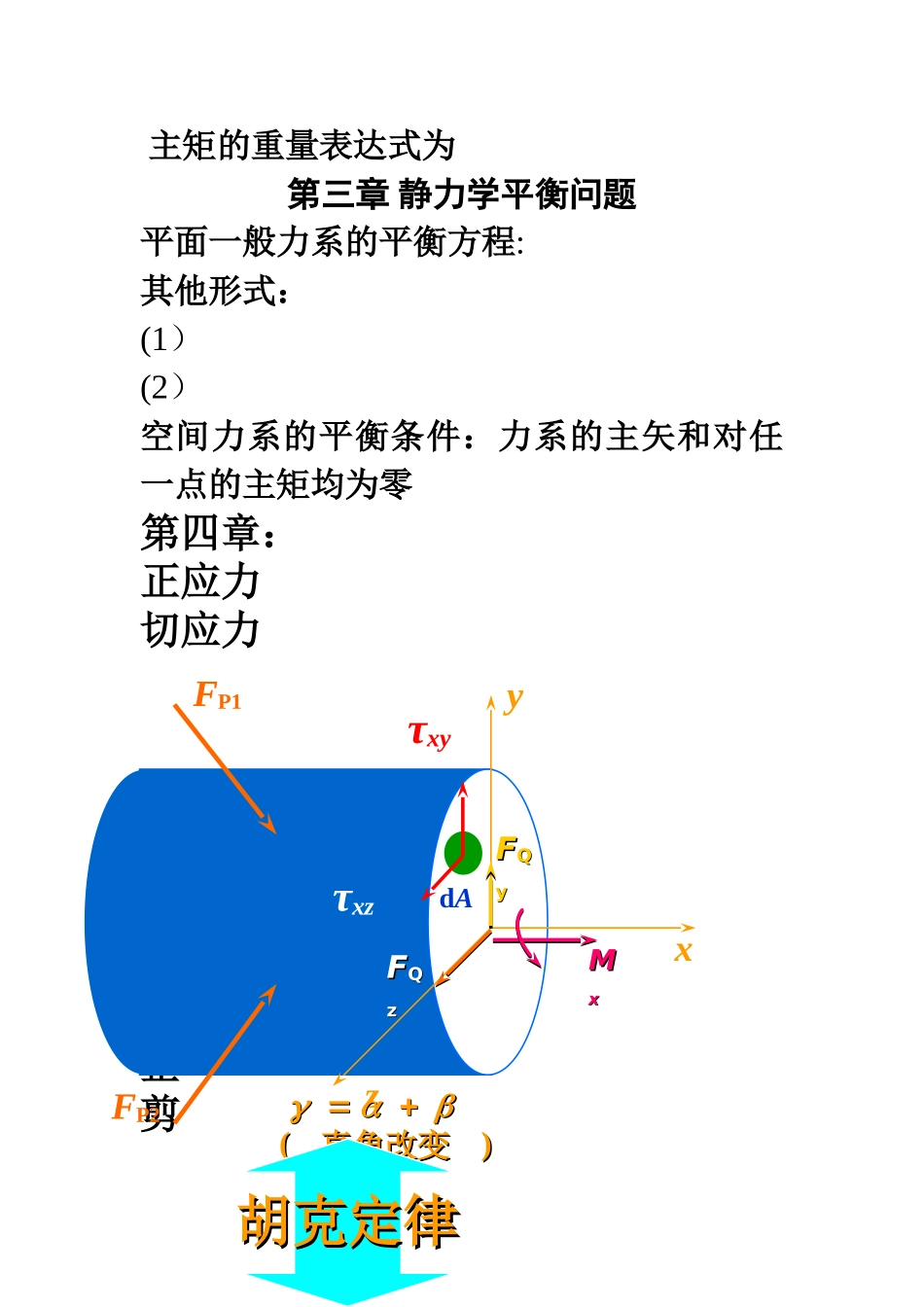
工程力学公式大全第一章:力矩用符号 MO(F)表示。即力矩矢量 描述力的转动效应力矩矢量的模描述转动效应的大小,它等于力的大小与矩心到力作用线的垂直距离(力臂)的乘积,即q 为矢径 r 与力 F 之间的夹角。平面力系的合力对平面上任一点之矩等于力系中所有的力对同一点之矩的代数和或者简写成力偶矩第二章:一主矢:有任意多个力所组成的力系(F1,F2…Fn),的矢量和:二主矩:力系中所有的力对同一点 O 之矩的矢量和用表示:空间任意汇交系在 oxyz 坐标中投影表达式:对于空间任意力系 主矩的重量表达式为第三章 静力学平衡问题平面一般力系的平衡方程:其他形式:(1)(2)空间力系的平衡条件:力系的主矢和对任一点的主矩均为零第四章:正应力切应力正应变剪应变FP1FP2yxz dAτxyτxzMMxxFFQQyyFFQQzz))((直角改变直角改变量量胡克定律胡克定律式中,E 和 G 为材料有关的弹性常数:E 为弹性模量或杨氏模量;G 为切变模量。第五章总结公式:1。正确画出轴力图,计算出各个截面的轴力2。注意拉压变形以及拉压产生的正应力和切应力其中 最大正应力发生在垂直于轴线处σα=pα=σ0cosα 最大切应力发生在与轴线成 45°角时 τα= pα=σ=根据胡克定律 σ=Eε 得 拉压变形 ∆l= (其中 EA 为拉压刚度)=∆b/b 泊松比 μ=-强度校核 σmax<[σ]同时 拉压变形满足叠加原理。可以通过拉压变形建立变形协调方程,解决拉压静不定问题第六章:作用于构件的外扭矩与机器的转速、功率有关。在传动轴计算中,通常给出传动功率P 和转速 n,则传动轴所受的外加扭力矩Me 可用下式计算:假如功率 P 的单位用马力(1 马力=735.5 N•m/s),则剪切胡克定律当在弹性范围内加载时,剪应力与剪应变成正比:式中式中 GIGIPP——扭转刚度;扭转刚度; IIPP——横截面的极惯性矩。横截面的极惯性矩。对于直径为 d 的实心圆截面对于内、外直径分别为 d 和 D 的圆环截面受扭圆轴的强度设计准则 第八章1。弹性范围内的挠度曲线在一点的曲率在这一点处横截面上的弯矩、弯曲刚度之间关系:EI————----—横截面的弯曲刚度2。梁在弯曲变形后,横截面的位置将发生改变,这种位置的改变称为位移(displacement)。梁的位移包括三部分:1)横截面形心沿水平方向的位移,称为轴向位移或水平位移(horizontal displacement),用 u 表示。2)横截面形心处的铅垂位移,称为挠度(deflection),用 w 表示;3)变形后...