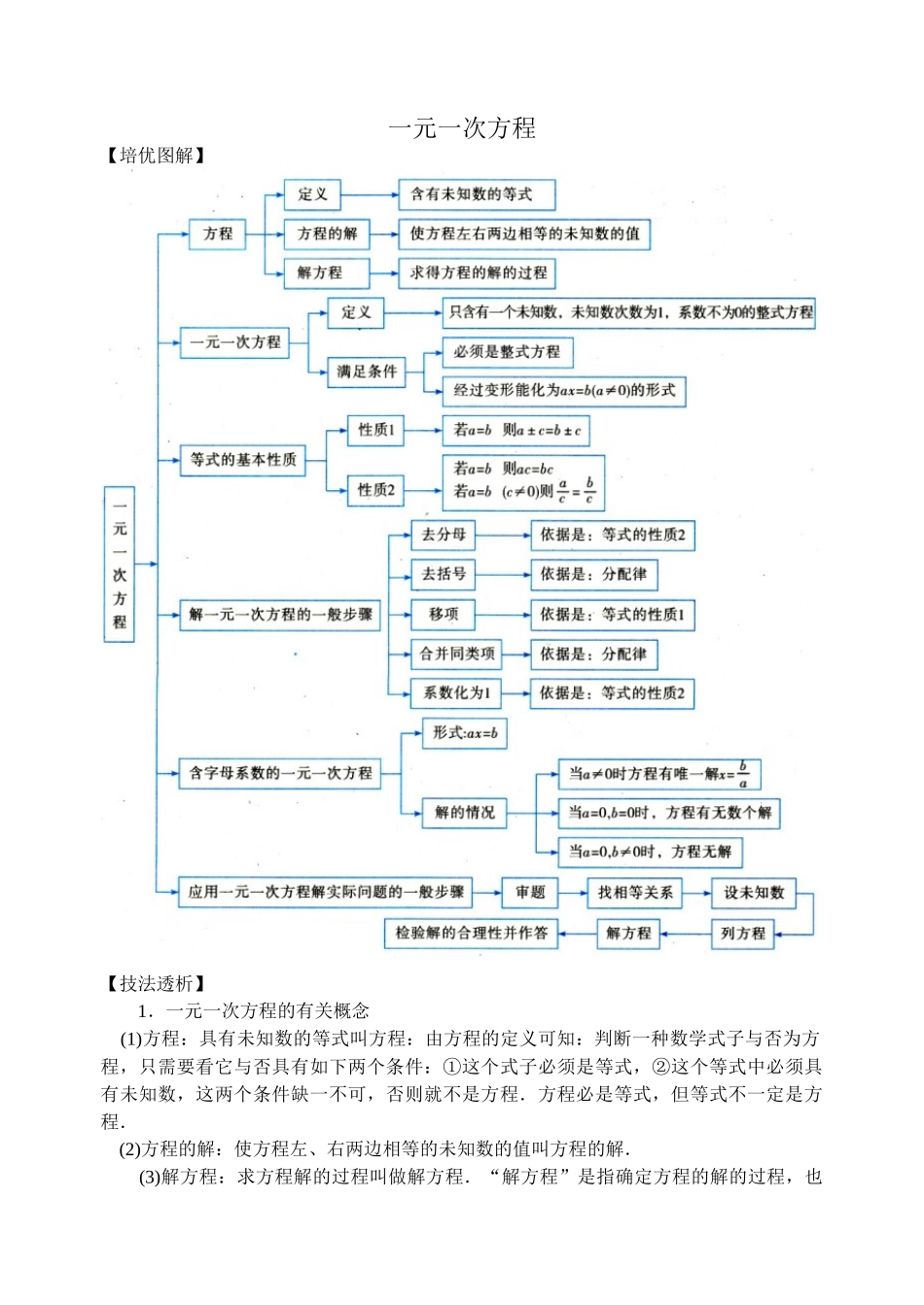
一元一次方程【培优图解】【技法透析】 1.一元一次方程的有关概念 (1)方程:具有未知数的等式叫方程:由方程的定义可知:判断一种数学式子与否为方程,只需要看它与否具有如下两个条件:①这个式子必须是等式,②这个等式中必须具有未知数,这两个条件缺一不可,否则就不是方程.方程必是等式,但等式不一定是方程. (2)方程的解:使方程左、右两边相等的未知数的值叫方程的解.(3)解方程:求方程解的过程叫做解方程.“解方程”是指确定方程的解的过程,也就是把方程进行变形的过程,因此,“解方程”与“方程的解”是两个完全不一样的概念. (4)一元一次方程:只具有一种未知数,未知数的次数为 1,这样的方程叫一元一次方程,判断一种方程是不是一元一次方程,必须具有如下三个条件:①必须是整式方程;②只具有一种未知数;③未知数的次数为 1,且系数不为 0.如方程 x-是分式方程而不是整式方程,方程 3x-2y=1 中具有两个未知数,方程 2x-5=x2+1 中未知数的最高次数为 2(次),因此,这三个方程都不是一元一次方程.像方程 5x-3=5(x-1),从表面上看,仿佛是一元一次方程,其实通过化简后这个方程变为-3=-5,就不是一元一次方程;而像方程 x2-2x-3=x2+5,表面上看它是一元二次方程,其实通过化简后,这个方程变为-2x=8,因此实际上它是一元一次方程.2.等式的性质 (1)等式的性质 1:等式的两边都加上(或减去)同一种数或同一种式子,所得的成果仍是等式,即:假如 a=b,则 a±c=b±c.(2)等式的性质 2:等式的两边都乘以(或除以)同一种不为 0 的数所得的成果仍是等式.即:假如 a=b,则 ac=bc,.(c≠0)3.解一元一次方程的一般环节 (1)去分母:即在方程的左、右两边都乘以各分母的最小公倍数,去公母的根据是等式的性质 2.去分母时要防止漏乘不含分母的项,同步要把分子(假如含几项)作为一种整体用括号括起来,以及分母约分后“1”省略不写. (2)去括号:去括号的根据是去括号法则及乘法分派律.去括号时先要分清括号前是“+”还是“-”号,不要弄错符号,还要防止漏乘括号里背面的项. (3)移项:移项是解方程常用的一种变形.移项的根据是等式的性质.一般是把具有未知数的项移到方程的左边,把不含未知数的项都移到方程的右边.注意移项一定要变号. (4)合并同类项:运用合并同类项法则,将方程化为 ax=b(a≠0)的形式.合并同类项的根据是乘法分派律. (5)系数化为 1...