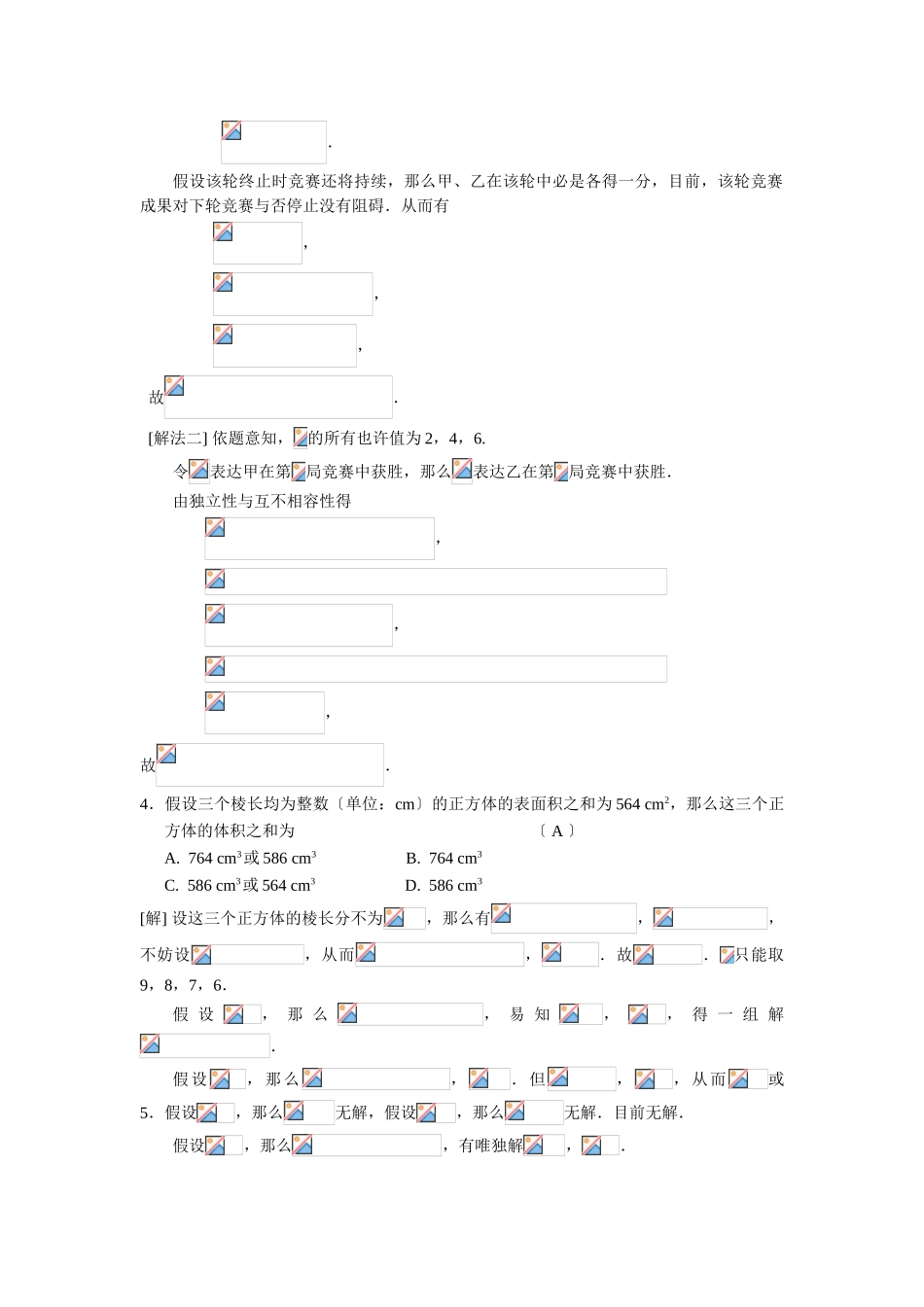
全国高中数学联合竞赛一试(A 卷)试题参照答案及评分原则〔A 卷〕讲明:1.评阅试卷时,请根据本评分原则.选择题只设 6 分和 0 分两档,填空题只设 9 分和 0 分两档;其他各题的评阅,请严格按照本评分原则的评分档次给分,不要增长其他中间档次.2.假如考生的解答措施和本解答不一样,只要思绪合理、环节对的,在评卷时可参照本评分原则合适划分档次评分,解答题中 5 分为一种档次,不要增长其他中间档次.一、选择题〔此题总分值 36 分,每题 6 分〕1.函数在上的最小值是 〔 C 〕A.0 B.1 C.2 D.3[解] 当时,,因此,当且仅当时上式取等号.而此方程有解,因此在上的最小值为 2.2.设,,假设,那么实数的取值范围为 〔 D 〕A. B. C. D.[解] 因有两个实根 ,,故等价于且,即且,解之得.3.甲乙两人进行乒乓球竞赛,约定每局胜者得 1 分,负者得 0 分,竞赛进行到有一人比对方多 2 分或打满 6 局时停止.设甲在每局中获胜的概率为,乙在每局中获胜的概率为,且各局胜负互相独立,那么竞赛停止时已打局数的期望为 〔 B 〕A. B. C. D. [解法一] 依题意知,的所有也许值为 2,4,6.设每两局竞赛为一轮,那么该轮终止时竞赛停止的概率为 .假设该轮终止时竞赛还将持续,那么甲、乙在该轮中必是各得一分,目前,该轮竞赛成果对下轮竞赛与否停止没有阻碍.从而有 , , ,故.[解法二] 依题意知,的所有也许值为 2,4,6.令表达甲在第局竞赛中获胜,那么表达乙在第局竞赛中获胜.由独立性与互不相容性得, , ,故.4.假设三个棱长均为整数〔单位:cm〕的正方体的表面积之和为 564 cm2,那么这三个正方体的体积之和为 〔 A 〕A. 764 cm3或 586 cm3 B. 764 cm3 C. 586 cm3或 564 cm3 D. 586 cm3[解] 设这三个正方体的棱长分不为,那么有,,不妨设,从而,.故.只能取9,8,7,6.假 设, 那 么, 易 知,, 得 一 组 解.假设,那么,.但,,从而或5.假设,那么无解,假设,那么无解.目前无解.假设,那么,有唯独解,.假设,那么,目前,.故,但,故,目前无解.综上,共有两组解或体积为cm3或cm3.5.方程组的有理数解的个数为 〔 B 〕A. 1 B. 2 C. 3 D. 4[解] 假设,那么解得或假设,那么由得. ①由得. ② 将②代入得. ③由①得,代入③化简得.易知无有理数根,故,由①得,由②得,与矛盾,故该方程组共有两组有理...