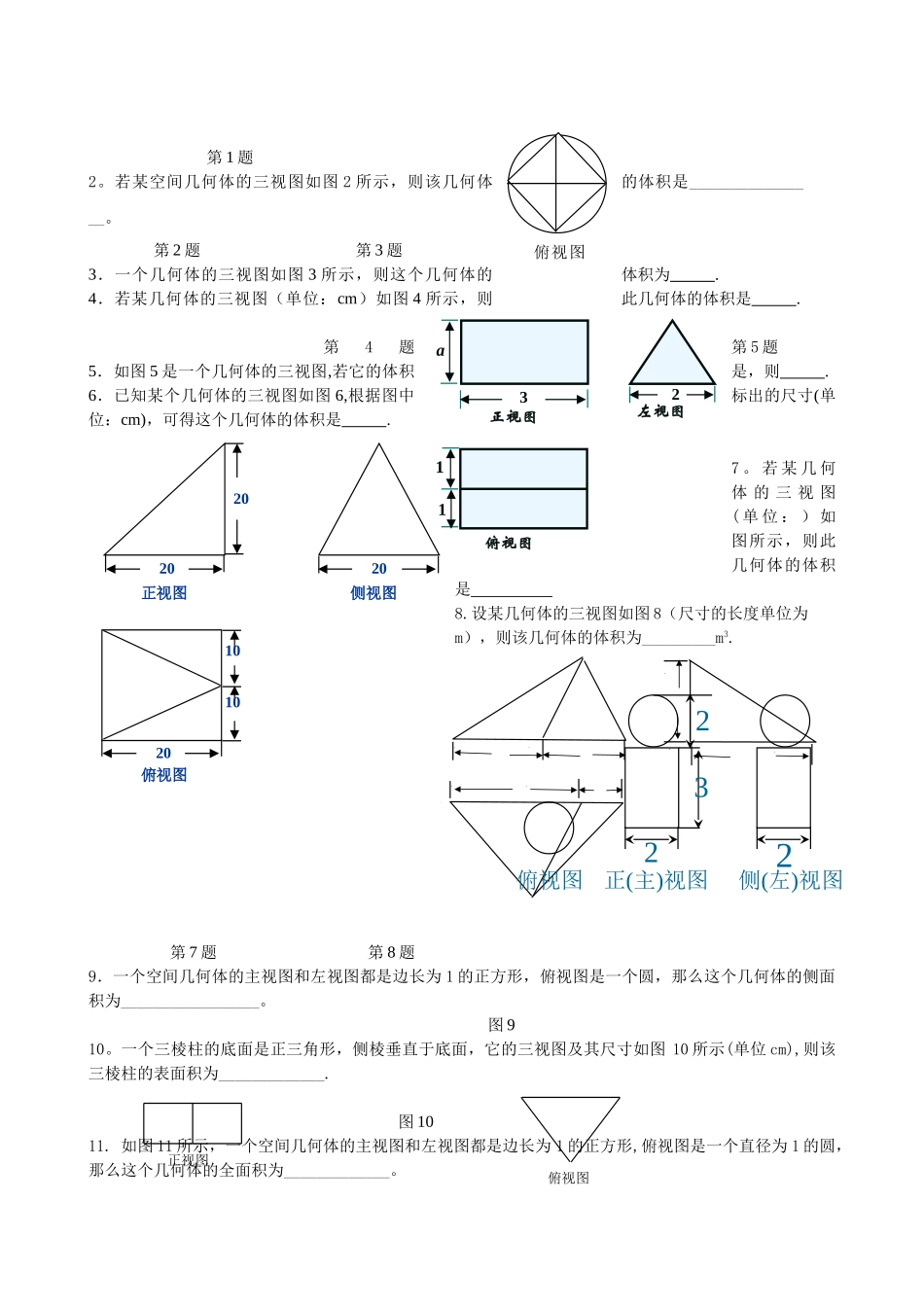
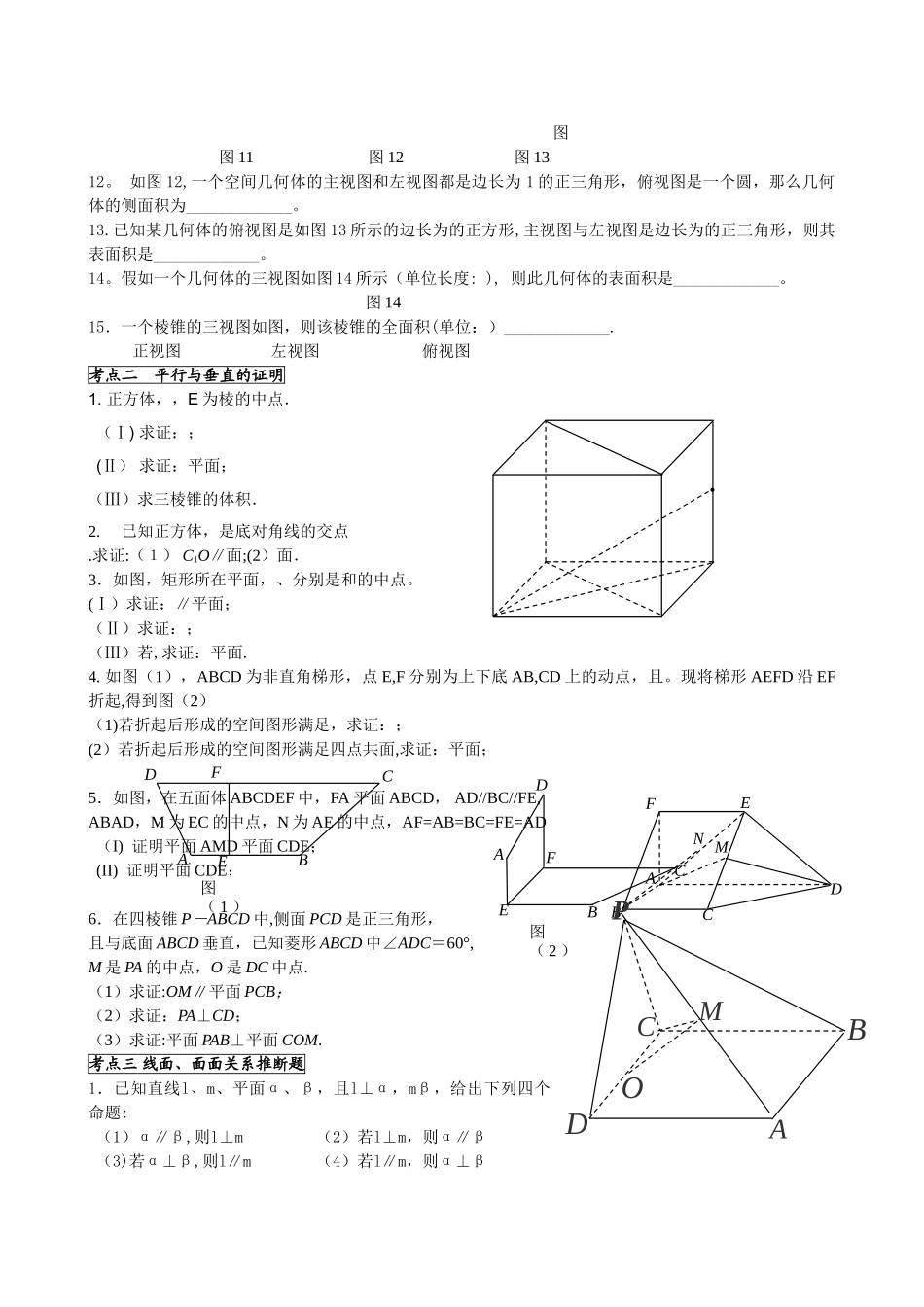
立体几何专题复习一、【知识总结】基本图形1.棱柱——有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。①②四棱柱 底面为平行四边形 平行六面体 侧棱垂直于底面 直平行六面体 底面为矩形 长方体 底面为正方形 正四棱柱 侧棱与底面边长相等 正方体2。 棱锥棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。 ★正棱锥——假如有一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥。3.球球的性质:①球心与截面圆心的连线垂直于截面;★②(其中,球心到截面的距离为 d、球的半径为 R、截面的半径为 r)★球与多面体的组合体:球与正四面体,球与长方体,球与正方体等的内接与外切。注:球的有关问题转化为圆的问题解决。球面积、体积公式:(其中 R 为球的半径)平行垂直基础知识网络★★★二、【典型例题】考点一:三视图1.一空间几何体的三视图如图 1 所示,则该几何体的体积为_________________.平行关系平面几何知识线线平行线面平行面面平行垂直关系平面几何知识线线垂直线面垂直面面垂直判定性质判定推论性质判定判定 性质判定面面垂直定义1.2.3.4.5.平行与垂直关系可互相转化2 2 侧 ( 左 ) 视图 2 2 2 正 ( 主 ) 视图 俯视图 第 1 题2。若某空间几何体的三视图如图 2 所示,则该几何体的体积是________________。第 2 题 第 3 题3.一个几何体的三视图如图 3 所示,则这个几何体的体积为 .4.若某几何体的三视图(单位:cm)如图 4 所示,则此几何体的体积是 . 第4题 第 5 题5.如图 5 是一个几何体的三视图,若它的体积是,则 .6.已知某个几何体的三视图如图 6,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 .7 。 若 某 几 何体 的 三 视 图( 单 位 : ) 如图所示,则此几何体的体积是 8.设某几何体的三视图如图 8(尺寸的长度单位为m),则该几何体的体积为_________m3. 第 7 题 第 8 题9.一个空间几何体的主视图和左视图都是边长为 1 的正方形,俯视图是一个圆,那么这个几何体的侧面积为_________________。图 910。一个三棱柱的底面是正三角形,侧棱垂直于底面,它的三视图及其尺寸如图 10 所示(单位 cm),则该三棱柱的表面积为_____________. 图 1011. 如图 11 所示,一个空...