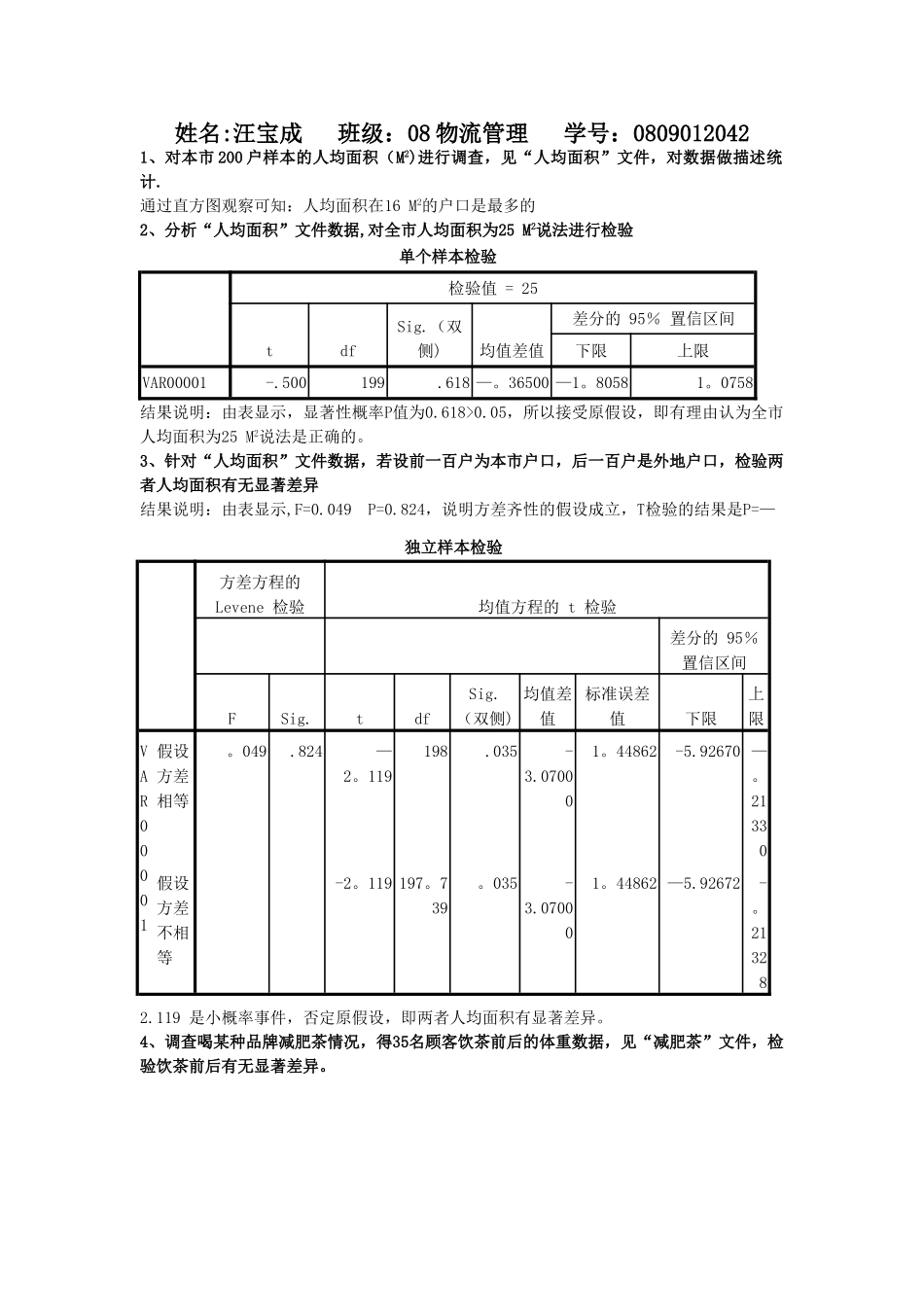
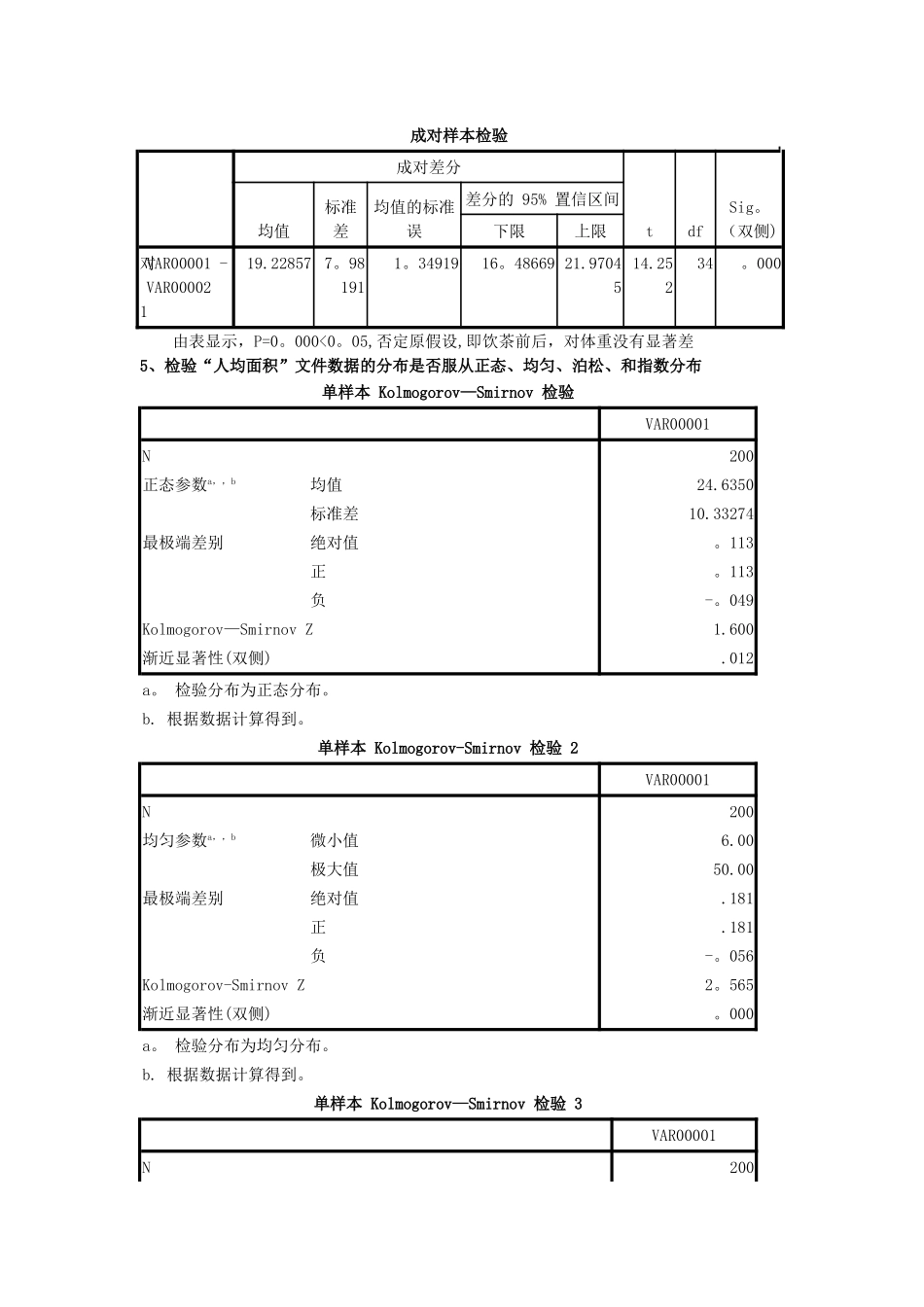
姓名:汪宝成 班级:08 物流管理 学号:08090120421、对本市 200 户样本的人均面积(M2)进行调查,见“人均面积”文件,对数据做描述统计.通过直方图观察可知:人均面积在16 M2的户口是最多的2、分析“人均面积”文件数据,对全市人均面积为25 M2说法进行检验单个样本检验检验值 = 25 tdfSig.(双侧)均值差值差分的 95% 置信区间下限上限VAR00001-.500199.618 —。36500 —1。80581。0758结果说明:由表显示,显著性概率P值为0.618>0.05,所以接受原假设,即有理由认为全市人均面积为25 M2说法是正确的。3、针对“人均面积”文件数据,若设前一百户为本市户口,后一百户是外地户口,检验两者人均面积有无显著差异结果说明:由表显示,F=0.049 P=0.824,说明方差齐性的假设成立,T检验的结果是P=—2.119 是小概率事件,否定原假设,即两者人均面积有显著差异。4、调查喝某种品牌减肥茶情况,得35名顾客饮茶前后的体重数据,见“减肥茶”文件,检验饮茶前后有无显著差异。独立样本检验方差方程的 Levene 检验均值方程的 t 检验差分的 95% 置信区间FSig.tdfSig.(双侧)均值差值标准误差值下限上限VAR00001假设方差相等。049.824—2。119198.035-3.070001。44862-5.92670 —。21330假设方差不相等-2。119 197。739。035-3.070001。44862 —5.92672-。21328成对样本检验成对差分tdfSig。(双侧)均值标准差均值的标准误差分的 95% 置信区间下限上限对 1VAR00001 - VAR0000219.22857 7。981911。3491916。48669 21.9704514.25234。000由表显示,P=0。000<0。05,否定原假设,即饮茶前后,对体重没有显著差5、检验“人均面积”文件数据的分布是否服从正态、均匀、泊松、和指数分布单样本 Kolmogorov—Smirnov 检验VAR00001N200正态参数a,,b均值24.6350标准差10.33274最极端差别绝对值。113正。113负-。049Kolmogorov—Smirnov Z1.600渐近显著性(双侧).012a。 检验分布为正态分布。b. 根据数据计算得到。单样本 Kolmogorov-Smirnov 检验 2VAR00001N200均匀参数a,,b微小值6.00极大值50.00最极端差别绝对值.181正.181负-。056Kolmogorov-Smirnov Z2。565渐近显著性(双侧)。000a。 检验分布为均匀分布。b. 根据数据计算得到。单样本 Kolmogorov—Smirnov 检验 3VAR00001N200单样本 Kolmogorov—Smirnov 检验VAR00001N200正态参数a,,b均值24.6350标准差10.33274最极端差别绝对值。113正。113负-。049Kolmog...