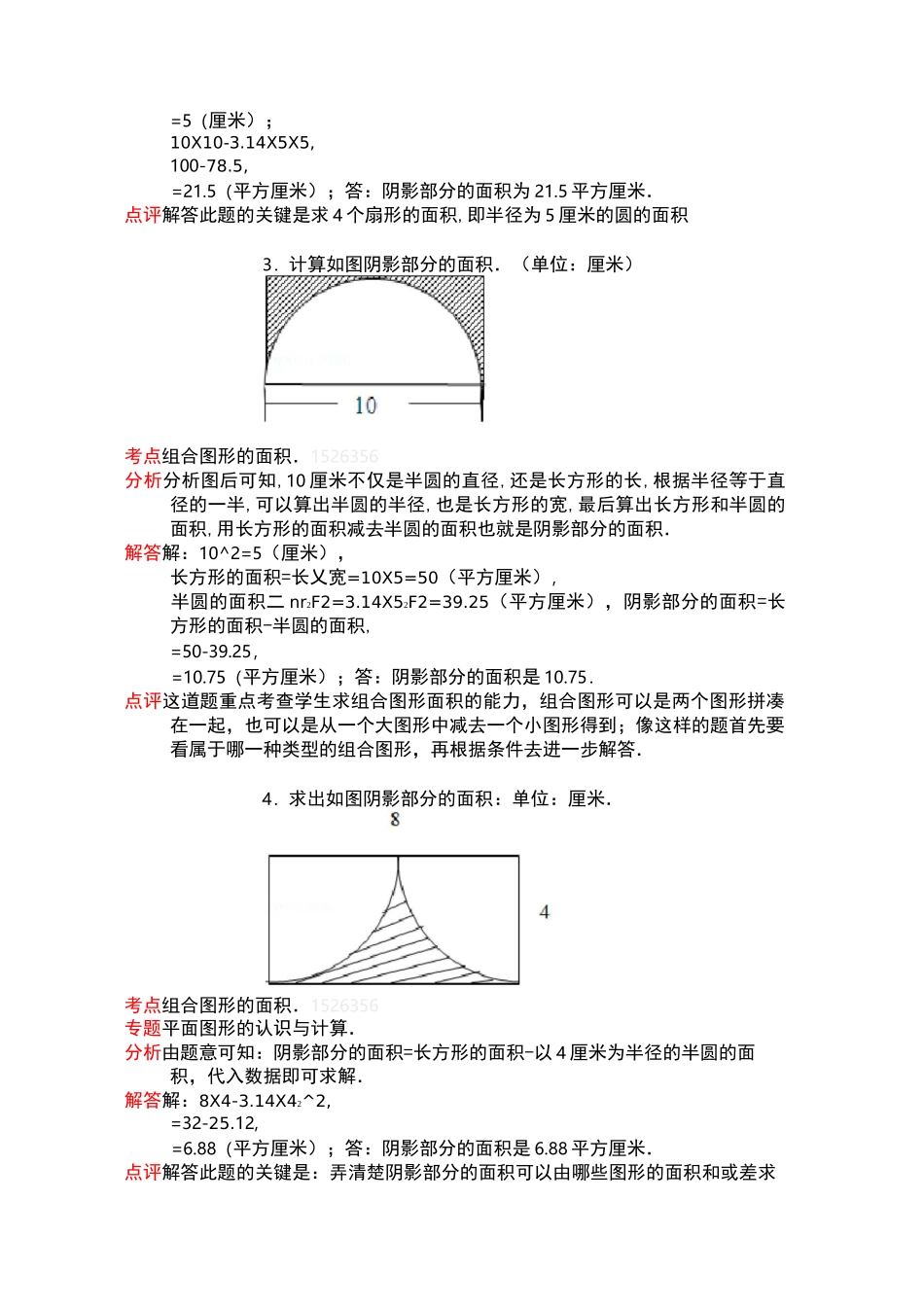
小升初阴影部分面积专题☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆试题解析1.求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积.1526356分析阴影部分的面积等于梯形的面积减去直径为 4 厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答解:(4+6)X4F2F2-3.14XF2,2=10-3.14X4F2,=10-6.28,=3.72(平方厘米);答:阴影部分的面积是 3.72 平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积.1526356分析根据图形可以看出:阴影部分的面积等于正方形的面积减去 4 个扇形的面积.正方形的面积等于(10X10)100 平方厘米,4 个扇形的面积等于半径为(10F2)5 厘米的圆的面积,即:3.14X5X5=78.5(平方厘米).解答解:扇形的半径是:10F2,=5(厘米);10X10-3.14X5X5,100-78.5,=21.5(平方厘米);答:阴影部分的面积为 21.5 平方厘米.点评解答此题的关键是求 4 个扇形的面积,即半径为 5 厘米的圆的面积3.计算如图阴影部分的面积.(单位:厘米)考点组合图形的面积.1526356分析分析图后可知,10 厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解:10^2=5(厘米),长方形的面积=长乂宽=10X5=50(平方厘米),半圆的面积二 nr2F2=3.14X52F2=39.25(平方厘米),阴影部分的面积=长方形的面积-半圆的面积,=50-39.25,=10.75(平方厘米);答:阴影部分的面积是 10.75.点评这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点组合图形的面积.1526356专题平面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积-以 4 厘米为半径的半圆的面积,代入数据即可求解.解答解:8X4-3.14X42^2,=32-25.12,=6.88(平方厘米);答:阴影部分的面积是 6.88 平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.5.求如图阴影部分的面积.(单位:厘米)考...