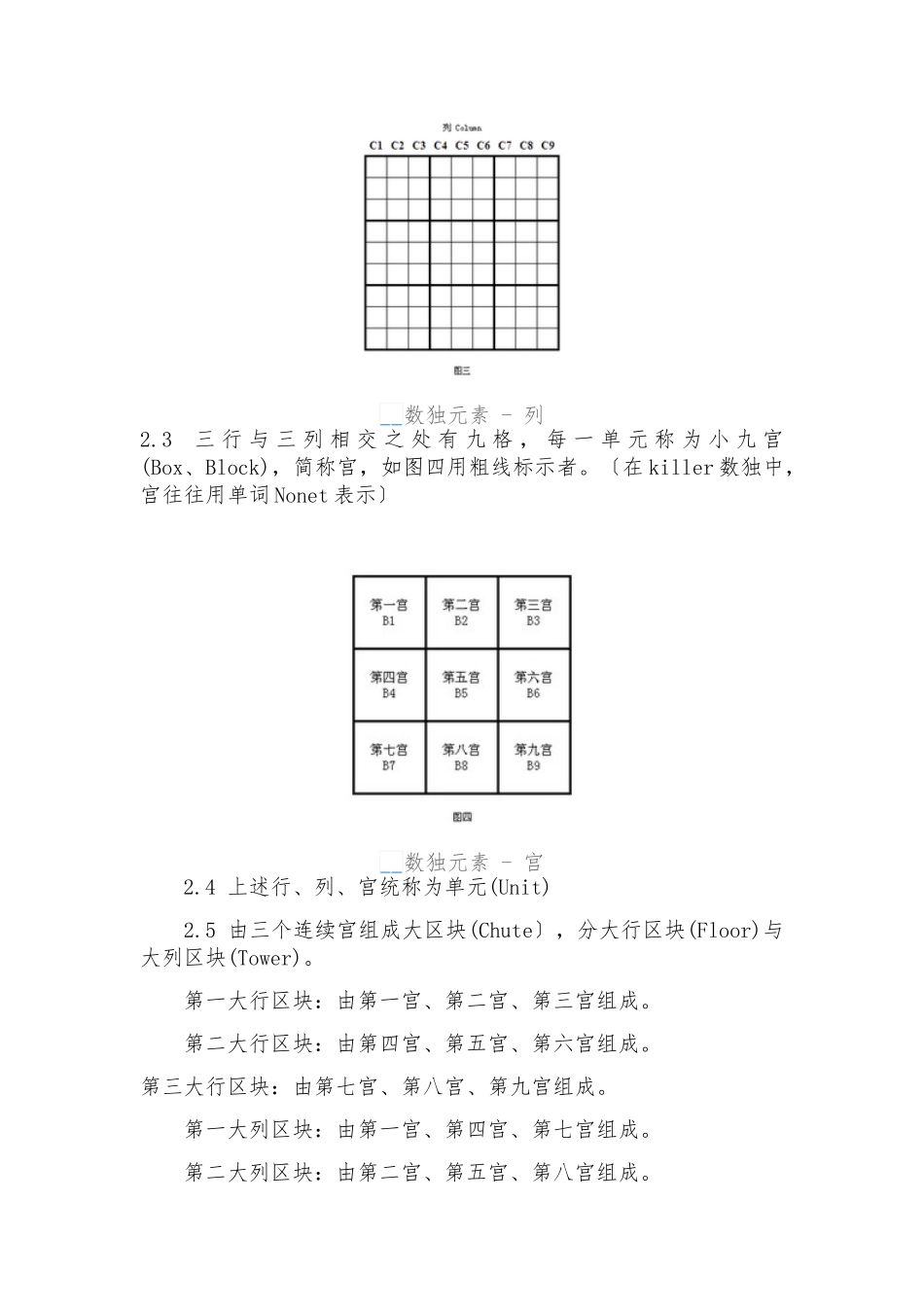
数独数独〔すうどく,Sudoku〕是一种运用纸、笔进展演算的逻辑游戏。玩家需要根据 9×9 盘面上的数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫的数字均含 1-9,不重复。 每一道合格的数独谜题都有且仅有唯一答案,推理方法也以此为根底,任何无解或多解的题目都是不合格的。起源 既然“数独〞有一个字是“数〞,人们也往往会联想到数学,那就不妨从大家都知道的数学家欧拉说起,但凡想了解数独历史的玩家在网络、书籍中搜索时,共同会提到的就是欧拉的“拉丁方块〔Latin square〕〞,如下列图: 拉丁方块的规那么:每一行〔Row〕、每一列〔Column〕均含1-N〔N 即盘面的规格〕,不重复。这与前面提到的标准数独非常相似,但少了一个宫的规那么。 其实说到这里,有些人会想到《易经》当中的洛书九宫图: 洛书九宫图横、竖、斜方向的三数之和均是 15,信任大家小学时候也都算过这个题目。所以也有人说数独的起源在中国。这点我们不得而知,但可以肯定的是,如今数独热潮已在全球蔓延。组成元素1.九宫格〔Grid〕 水平方向有九横行,垂直方向有九纵列的矩形,画分八十一个小矩形,称为九宫格(Grid),如图一所示,是数独(Sudoku)的作用围。 数独元素 - 九宫格[1]2.单元(Unit)画分 2.1 水平方向的每一横行有九格,每一横行称为行(Row),编号如图二所示。 数独元素 - 单元 2.2 垂直方向的每一纵列有九格,每一纵列称为列(Column),编号如图三所示。 数独元素 - 列2.3 三 行 与 三 列 相 交 之 处 有 九 格 , 每 一 单 元 称 为 小 九 宫(Box、Block),简称宫,如图四用粗线标示者。〔在 killer 数独中,宫往往用单词 Nonet 表示〕 数独元素 - 宫 2.4 上述行、列、宫统称为单元(Unit) 2.5 由三个连续宫组成大区块(Chute〕,分大行区块(Floor)与大列区块(Tower)。 第一大行区块:由第一宫、第二宫、第三宫组成。 第二大行区块:由第四宫、第五宫、第六宫组成。第三大行区块:由第七宫、第八宫、第九宫组成。 第一大列区块:由第一宫、第四宫、第七宫组成。 第二大列区块:由第二宫、第五宫、第八宫组成。 第三大列区块:由第三宫、第六宫、第九宫组成。3.格位(Cell)编号 格位按所处的行列单元给予坐标值,如图五所示。 数独元素 - 格位 坐标有多种标示法,有横行 A..I,纵列 1..9〔如中国〕,也有横行 1..9,纵列 A..I〔如日本〕,这两种标示容易混淆,故...