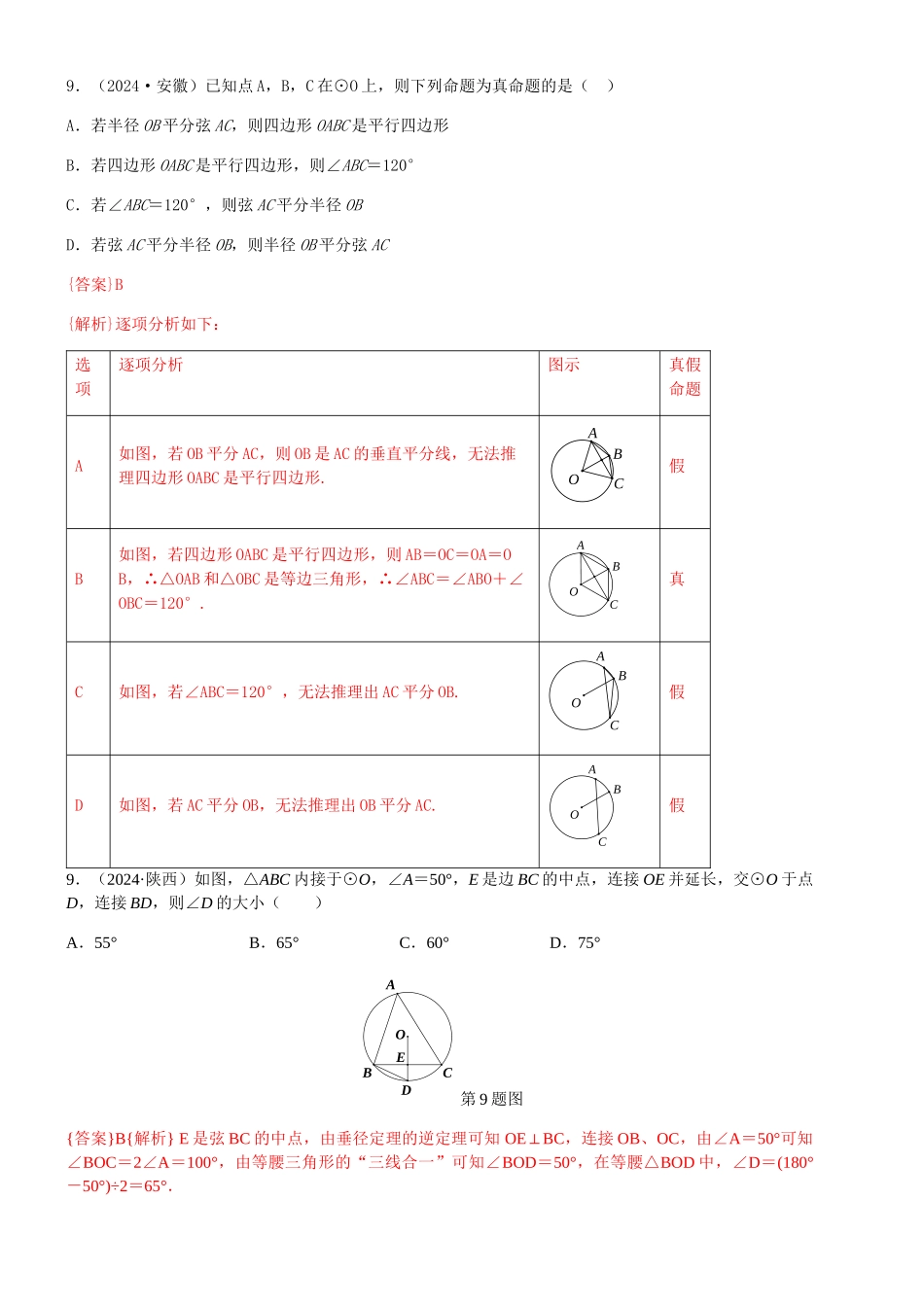
一、选择题9.(2024·杭州)如图,已知 BC 是的直径,半径,点 D 在劣弧 AC 上(不与点 A,点 C重合),BD 与 OA 交于点 E.设,,则( )A.3α+β=180°B.2α+β=180°C.3α-β=90°D . 2α - β = 90°{答案}D{解析}本题考查了同圆的半径相等,三角形的内角和定理以及三角形的外角.因为 OABC⊥,所以∠AOB=90°.因为 OB=OD,所以∠B=∠D.在△OBD 中,∠B+∠D+∠BOD=180°,即 2D∠ +90°+β=180°,所以 2D∠ +β=90°.因为∠AED 是△ODE 的外角,所以∠D=∠AED-∠AOD=α-β,所以 2(α-β)+β=90°,整理,得 2α-β=90°,因此本题选 D.4.(2024·绍兴)如图.点 A,B,C,D,E 均在⊙O 上.∠BAC=15°,∠CED=30°,则∠BOD 的度数为( )A.45°B.60°C.75°D.90°{答案}D{解析}本题考查了圆周角、圆心角以及它们所对的弧的度数之间的关系.在同圆中,圆周角的度数等于它所对的弧的度数的一半,圆心角的度数等于它所对的弧的度数,因为∠BAC=15°,∠CED=30°,所以弧 BC 是 30°,弧 CD 是 60°,则弧 BD 是 90°,故它所对的圆心角∠BOD 的度数是 90°.因此本题选 D.4.(2024 湖州)如图,已知四边形 ABCD 内接于⊙O,∠ABC=70°,则∠ADC 的度数是( )A.70°B.110°C.130°D.140°【分析】根据圆内接四边形的性质即可得到结论.【解答】解: 四边形 ABCD 内接于⊙O,∠ABC=70°,∴∠ADC=180°ABC﹣∠=180°70°﹣=110°,故选:B.7.(2024·黔东南州)如图,⊙O 的直径 CD=20,AB 是⊙O 的弦,AB⊥CD,垂足为 M,OM:OC=3:5,则 AB 的长为( )A.8B.12C.16D.2❑√91{答案}C {解析}如图,连接 OA,O ⊙的直径 CD=20,OM:OD=3:5,∴OD=10,OM=6.ABCD ⊥,∴AM¿❑√OA2−OM2=❑√102−62=¿8,∴AB=2AM=16.AEDOCB9.(2024·安徽)已知点 A,B,C 在⊙O 上,则下列命题为真命题的是( )A.若半径 OB 平分弦 AC,则四边形 OABC 是平行四边形B.若四边形 OABC 是平行四边形,则∠ABC=120°C.若∠ABC=120°,则弦 AC 平分半径 OBD.若弦 AC 平分半径 OB,则半径 OB 平分弦 AC {答案}B{解析}逐项分析如下:选项逐项分析图示真假命题A如图,若 OB 平分 AC,则 OB 是 AC 的垂直平分线,无法推理四边形 OABC 是平行四边形.ABCO假B如图,若四边形 OABC 是平...