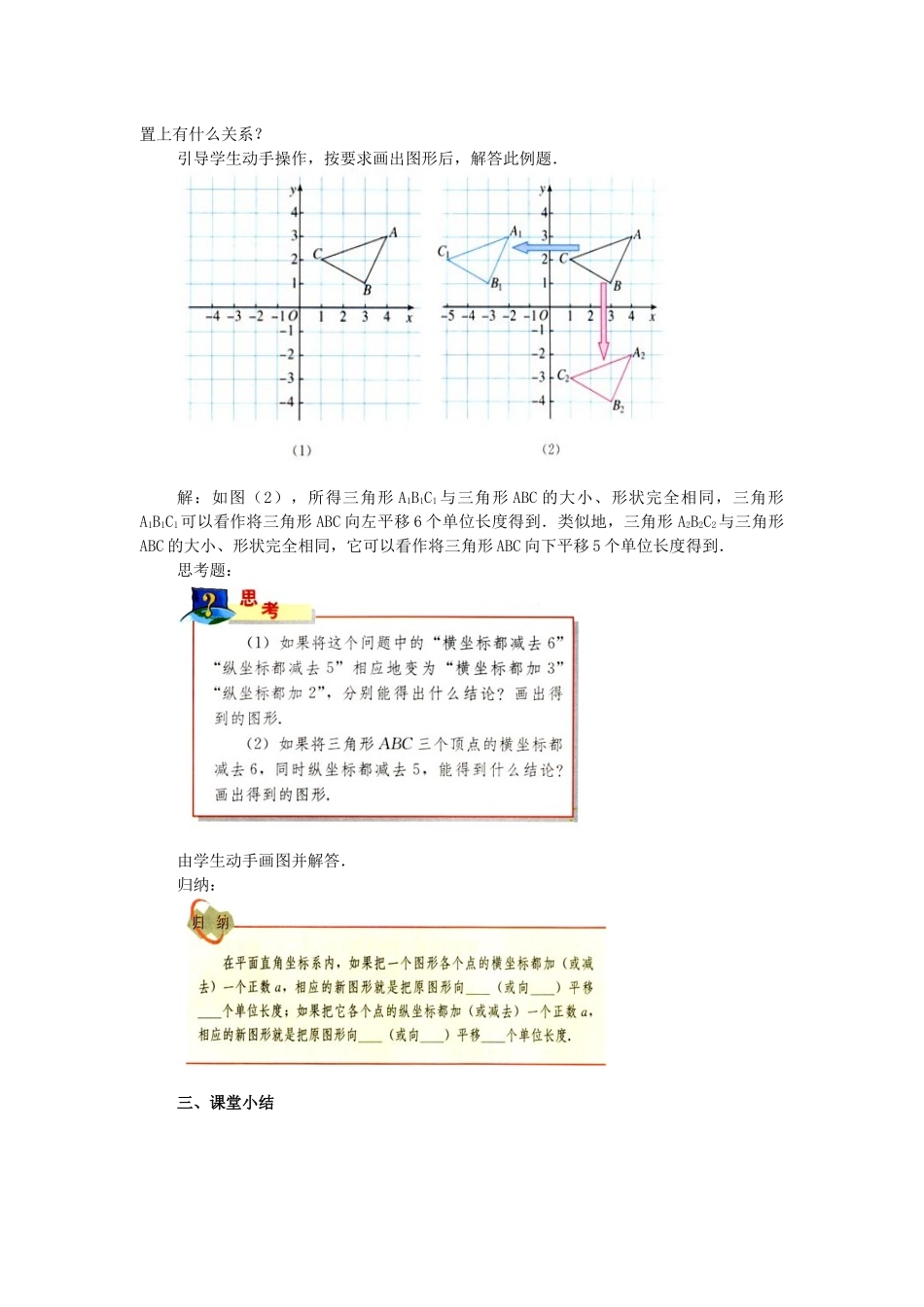
7.2.2 用坐标表示平移【教学目标】1.掌握坐标变化与图形平移的关系;能利用点的平移规律将平面图形进行平移;会根据图形上点的坐标的变化,来判定图形的移动过程.2.进展学生的形象思维能力,和数形结合的意识.3.用坐标表示平移体现了平面直角坐标系在数学中的应用.4.培育学生探究的兴趣和归纳概括的能力,体会使复杂问题简单化.【教学重点与难点】1.重点:掌握坐标变化与图形平移的关系.2.难点:利用坐标变化与图形平移的关系解决实际问题.【教学过程】一、引言上节课我们学习了用坐标表示地理位置,本节课我们继续讨论坐标方法的另一个应用.二、新课展示问题:(1)如图将点 A(-2,-3)向右平移 5 个单位长度,得到点 A1,在图上标出它的坐标,把点 A 向上平移 4 个单位长度呢?(2)把点 A 向左或向下平移 4 个单位长度,观察他们的变化,你能从中发现什么规律吗?(3)再找几个点,对他们进行平移,观察他们的坐标是否按你发现的规律变化?规律:在平面直角坐标系中,将点(x,y)向右(或左)平移 a 个单位长度,可以得到对应点(x+a,y)(或( , ));将点(x,y)向上(或下)平移 b 个单位长度,可以得到对应点(x,y+b)(或( , )).老师说明:对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;反过来,从图形上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移.例 如 图 ( 1 ) , 三 角 形ABC三 个 顶 点 坐 标 分 别 是A(4,3),B(3,1),C(1,2).( 1 ) 将 三 角 形 ABC 三 个 顶 点 的 横 坐 标 后 减 去 6 , 纵 坐 标 不 变 , 分 别 得 到 点A1、B1、C1,依次连接 A1、B1、C1各点,所得三角形 A1B1C1与三角形 ABC 的大小、形状和位置上有什么关系?( 2 ) 将 三 角 形 ABC 三 个 顶 点 的 纵 坐 标 都 减 去 5 , 横 坐 标 不 变 , 分 别 得 到 点A2、B2、C2,依次连接 A2、B2、C2各点,所得三角形 A2B2C2与三角形 ABC 的大小、形状和位置上有什么关系?引导学生动手操作,按要求画出图形后,解答此例题.解:如图(2),所得三角形 A1B1C1 与三角形 ABC 的大小、形状完全相同,三角形A1B1C1可以看作将三角形 ABC 向左平移 6 个单位长度得到.类似地,三角形 A2B2C2与三角形ABC 的大小、形状完全相同,它可以看作将三角形 ABC 向下平移 5 个单位长度得到.思考题:由学生动手画图并解答.归纳:三、课堂小结