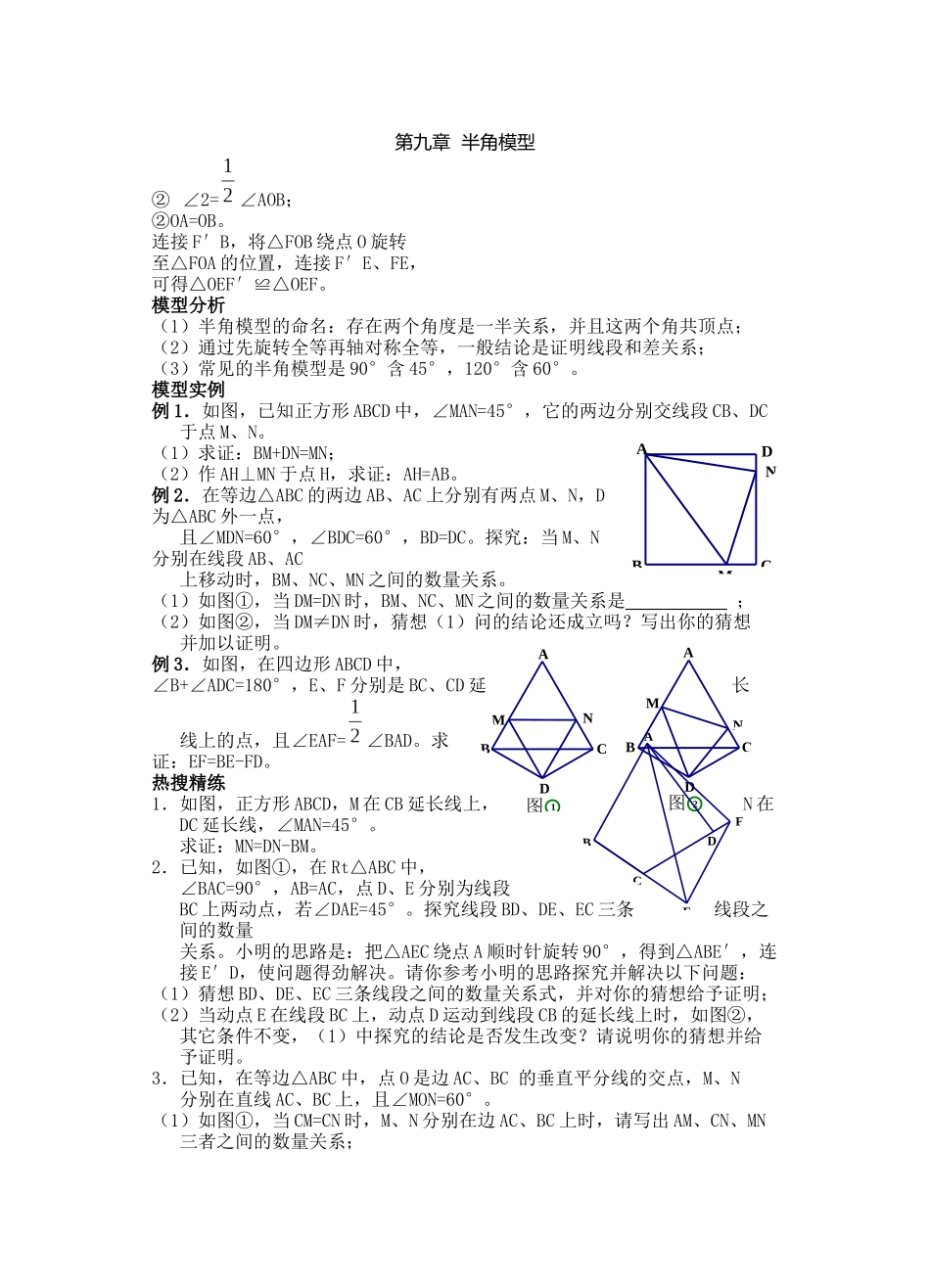
第九章 半角模型② ∠2=∠AOB;②OA=OB。连接 F′B,将△FOB 绕点 O 旋转至△FOA 的位置,连接 F′E、FE,可得△OEF′≌△OEF。模型分析(1)半角模型的命名:存在两个角度是一半关系,并且这两个角共顶点;(2)通过先旋转全等再轴对称全等,一般结论是证明线段和差关系;(3)常见的半角模型是 90°含 45°,120°含 60°。模型实例例 1.如图,已知正方形 ABCD 中,∠MAN=45°,它的两边分别交线段 CB、DC 于点 M、N。(1)求证:BM+DN=MN;(2)作 AH⊥MN 于点 H,求证:AH=AB。例 2.在等边△ABC 的两边 AB、AC 上分别有两点 M、N,D为△ABC 外一点, 且∠MDN=60°,∠BDC=60°,BD=DC。探究:当 M、N分别在线段 AB、AC上移动时,BM、NC、MN 之间的数量关系。(1)如图①,当 DM=DN 时,BM、NC、MN 之间的数量关系是 ;(2)如图②,当 DM≠DN 时,猜想(1)问的结论还成立吗?写出你的猜想 并加以证明。例 3.如图,在四边形 ABCD 中,∠B+∠ADC=180°,E、F 分别是 BC、CD 延长 线上的点,且∠EAF=∠BAD。求证:EF=BE-FD。热搜精练1.如图,正方形 ABCD,M 在 CB 延长线上,N 在DC 延长线,∠MAN=45°。 求证:MN=DN-BM。2.已知,如图①,在 Rt△ABC 中,∠BAC=90°,AB=AC,点 D、E 分别为线段 BC 上两动点,若∠DAE=45°。探究线段 BD、DE、EC 三条线段之间的数量 关系。小明的思路是:把△AEC 绕点 A 顺时针旋转 90°,得到△ABE′,连接 E′D,使问题得劲解决。请你参考小明的思路探究并解决以下问题:(1)猜想 BD、DE、EC 三条线段之间的数量关系式,并对你的猜想给予证明;(2)当动点 E 在线段 BC 上,动点 D 运动到线段 CB 的延长线上时,如图②, 其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明。3.已知,在等边△ABC 中,点 O 是边 AC、BC 的垂直平分线的交点,M、N 分别在直线 AC、BC 上,且∠MON=60°。(1)如图①,当 CM=CN 时,M、N 分别在边 AC、BC 上时,请写出 AM、CN、MN 三者之间的数量关系;DCBAMN图 2AMBDCN1图BACDMNAFEBCD(2)如图②,当 CM≠CN 时,M、N 分别在边 AC、BC 上时,(1)中的结论是否仍然成立?若成立,请你加以证明;若不成立,请说明理由;(3)如图③,当点 M 在边 AC 上,点 N 在 BC 的延长线上时,请直接写出线段AM、CN、MN 三者之间的数量关系。4.如...