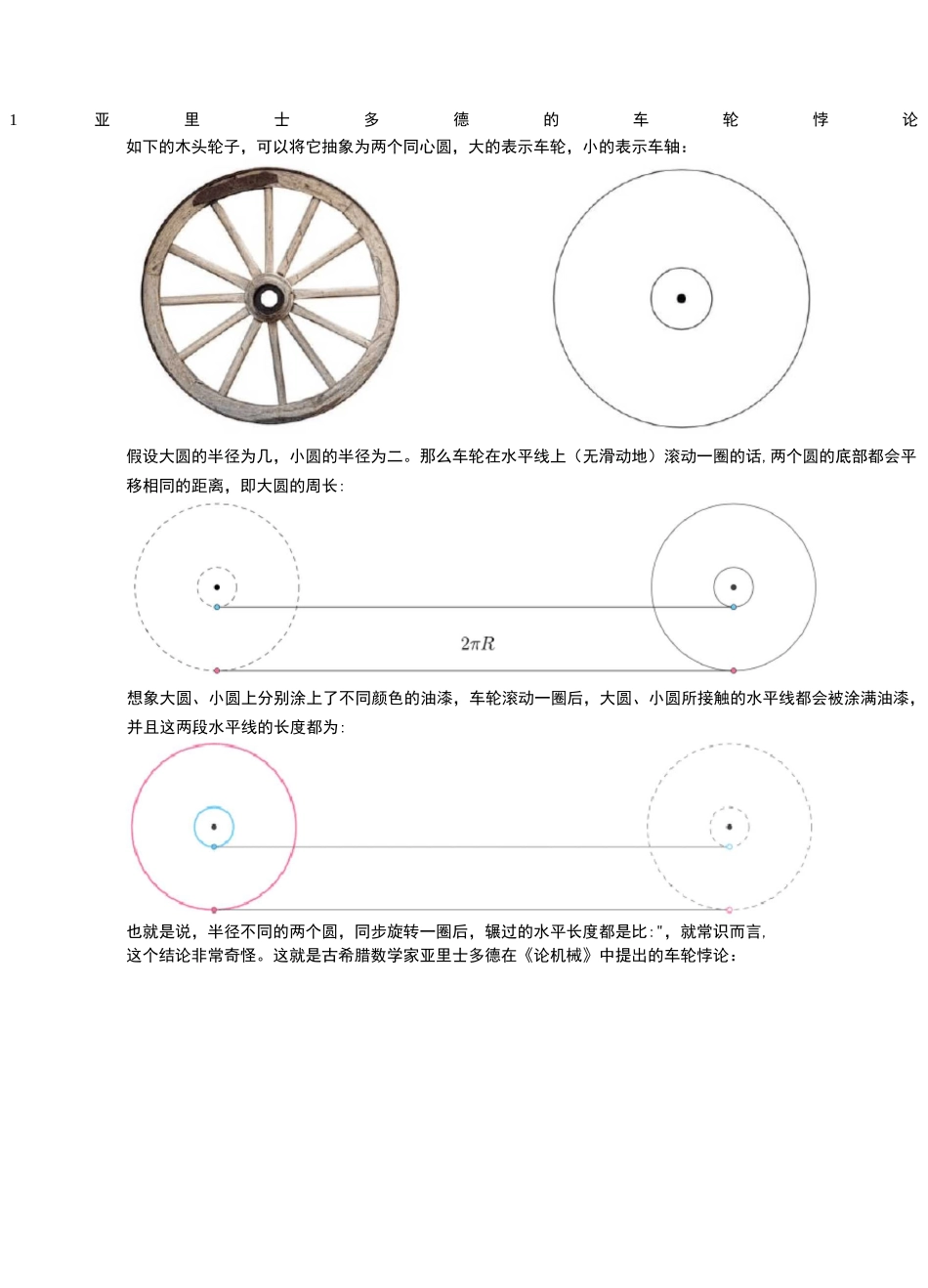
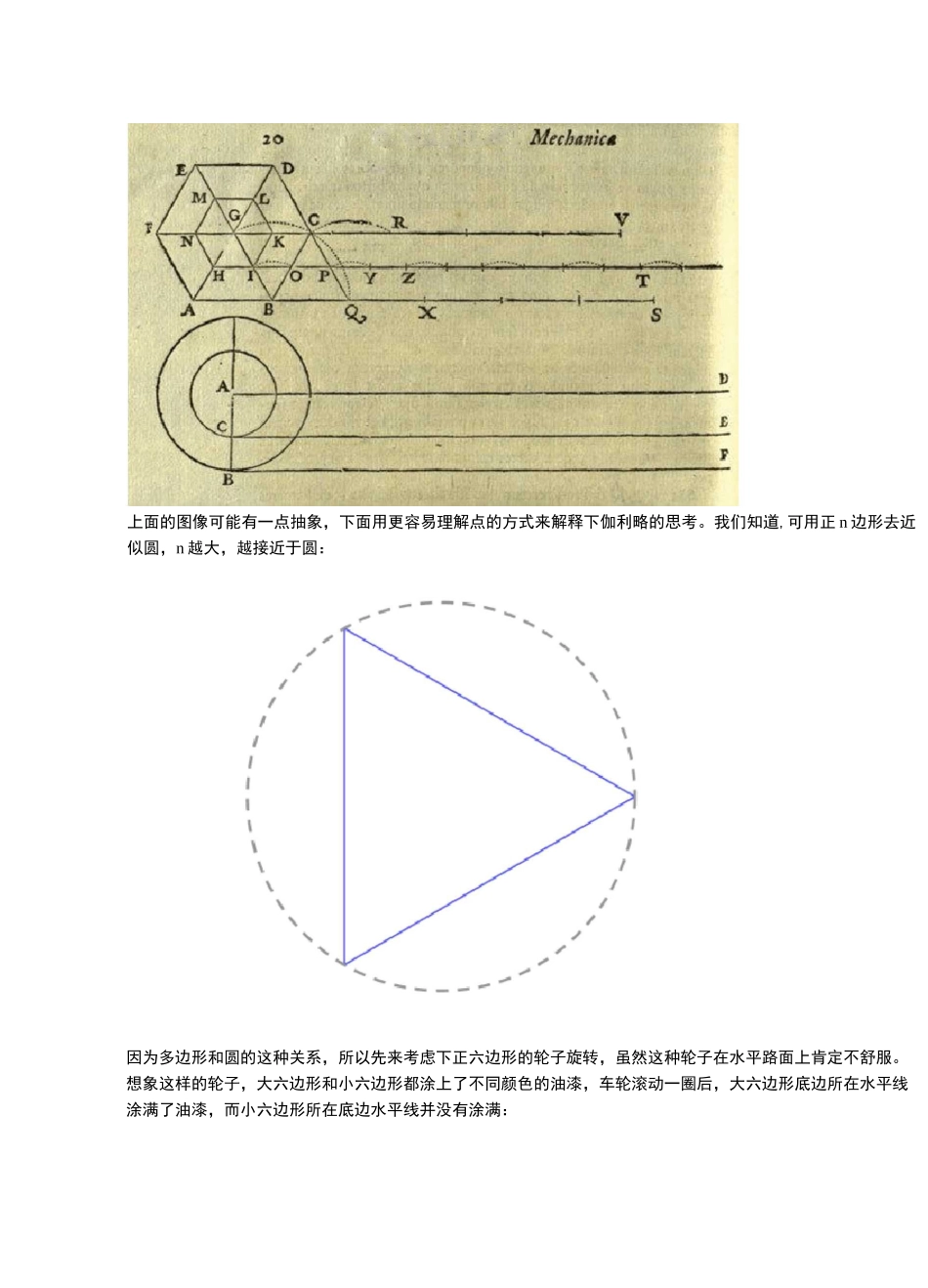
1亚里士多德的车轮悖论如下的木头轮子,可以将它抽象为两个同心圆,大的表示车轮,小的表示车轴:假设大圆的半径为几,小圆的半径为二。那么车轮在水平线上(无滑动地)滚动一圈的话,两个圆的底部都会平移相同的距离,即大圆的周长:想象大圆、小圆上分别涂上了不同颜色的油漆,车轮滚动一圈后,大圆、小圆所接触的水平线都会被涂满油漆,并且这两段水平线的长度都为:也就是说,半径不同的两个圆,同步旋转一圈后,辗过的水平长度都是比:",就常识而言,这个结论非常奇怪。这就是古希腊数学家亚里士多德在《论机械》中提出的车轮悖论:ARLSTOTELISMECHANICS,emendate,Xatiaa&Gommen 俎卅isilluftl'dtd・ABHEN'RLSMQy^^rF/pLlQ2\d^licQt&P呼呼評仏2 伽利略的思考1638 年出版的《论两种新科学及其数学演化》中,伽利略在其中提到了如何解释亚里士多德的车轮悖论:fAItTT•:!.5VLillHl'bTi.fill'(LgHoEtl>W51lDnEi^—泌.匕,K 亡丄爼-r■or_.jciynjtt/r.t