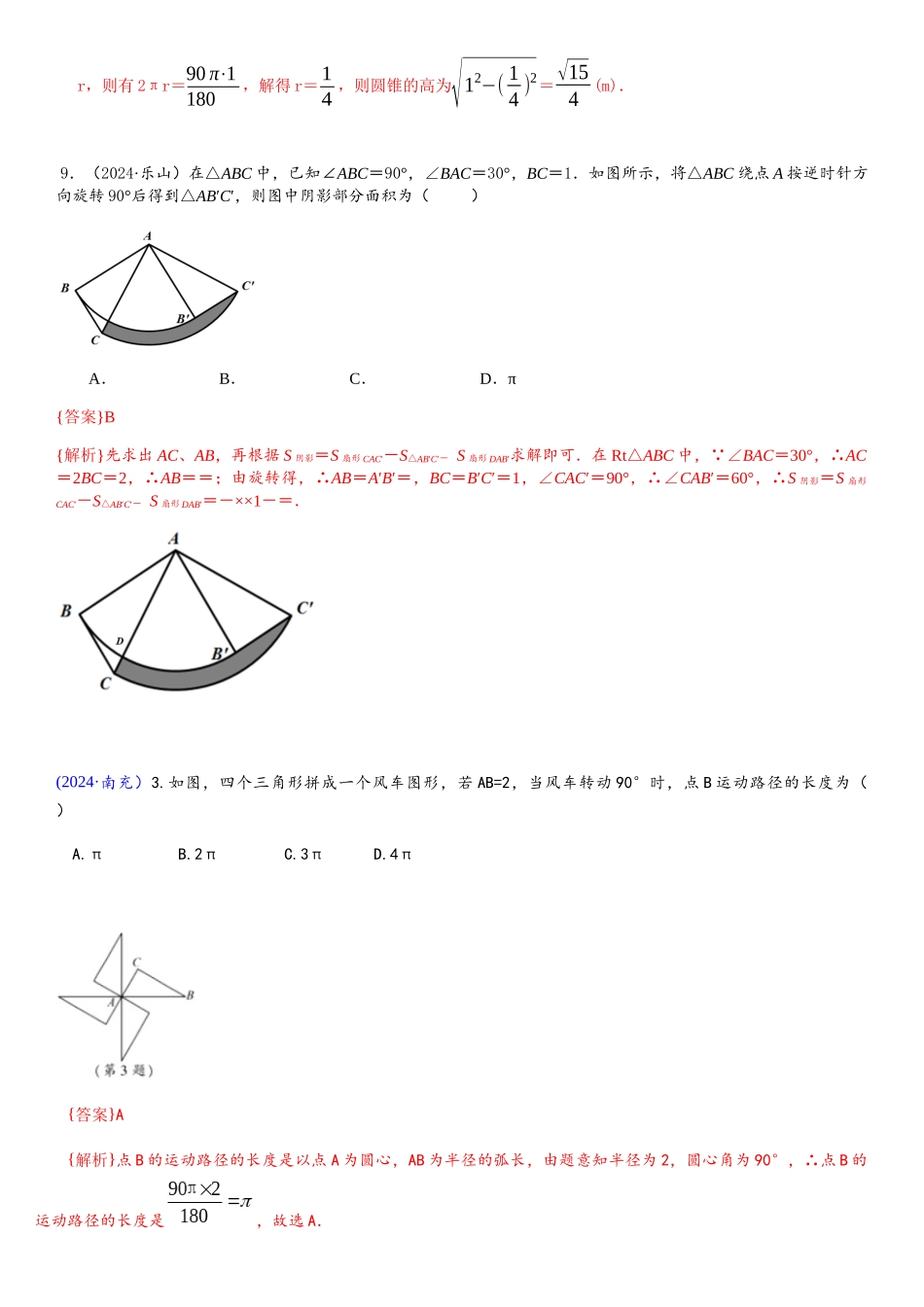
一、选择题8.(2024·苏州)如图,在扇形中,已知,,过的中点作,,垂足分别为、,则图中阴影部分的面积为( )A.B.C.D.{答案}B{解析}本题考查了不规则图形面积的计算,连接 OC,由题意得∠DOC=∠BOC=45°,四边形 OECD 为正方形,OC=,由特别角的三角函数得 OE=OD=1,S 阴影=S 扇形 OAB-S 正方形 CEOD=-12=-1,因此本题选 B.9.(2024·聊城)如图,AB 是⊙O 的直径,弦 CD⊥AB,垂足为点 M,连接 OC,DB,假如 OC∥DB,OC=2√3,那么图中阴影部分的面积是( )A.π B.2π C.3π D.4π{答案}B{解析}借助圆的性质,利用等积转化求解阴影部分的面积.由垂径定理,得 CM=DM, OC∥DB,∴∠C=∠D,又 ∠OMC=∠BMD,∴△OMC≌△BMD(ASA),∴OM=BM=12 OB=12 OC,∴cos∠COM=OMOC =12 ,∴∠COM=60°.∴S 阴影=S 扇形 BOC=60 π⋅(2√3)2360=2π.10.(2024·聊城)如图,有一块半径为 1m,圆心角为 90°的扇形铁皮,要把它做成一个圆锥形容器(接缝忽略不计),那么这个圆锥形容器的高为( )A.14m B.34m C.√154m D.√32m{答案}C{解析}先利用弧长公式求得圆锥的底面半径,再利用勾股定理求圆锥的高.设圆锥形容器底面圆的半径为D B C M O A r,则有 2πr=90 π⋅1180,解得 r=14,则圆锥的高为√12−( 14 )2=√154(m). 9.(2024·乐山)在△ABC 中,已知∠ABC=90°,∠BAC=30°,BC=1.如图所示,将△ABC 绕点 A 按逆时针方向旋转 90°后得到△AB′C′,则图中阴影部分面积为( )A.B.C.D.π{答案}B{解析}先求出 AC、AB,再根据 S 阴影=S 扇形 CAC′-S△AB′C′- S 扇形 DAB′求解即可.在 Rt△ABC 中, ∠BAC=30°,∴AC=2BC=2,∴AB==;由旋转得,∴AB=A′B′=,BC=B′C′=1,∠CAC′=90°,∴∠CAB′=60°,∴S 阴影=S 扇形CAC′-S△AB′C′- S 扇形 DAB′=-××1-=.(2024·南充)3.如图,四个三角形拼成一个风车图形,若 AB=2,当风车转动 90°时,点 B 运动路径的长度为( )A.π B.2π C.3π D.4π{答案}A{解析}点 B 的运动路径的长度是以点 A 为圆心,AB 为半径的弧长,由题意知半径为 2,圆心角为 90°,∴点 B 的运动路径的长度是,故选 A.(2024·德州)10.如图,圆内接正六边形的边长为 4,以其各边为直径作半圆,则图中阴影部分的面积为A. B. C. D. {答案}A{ 解 析 } 如 ...