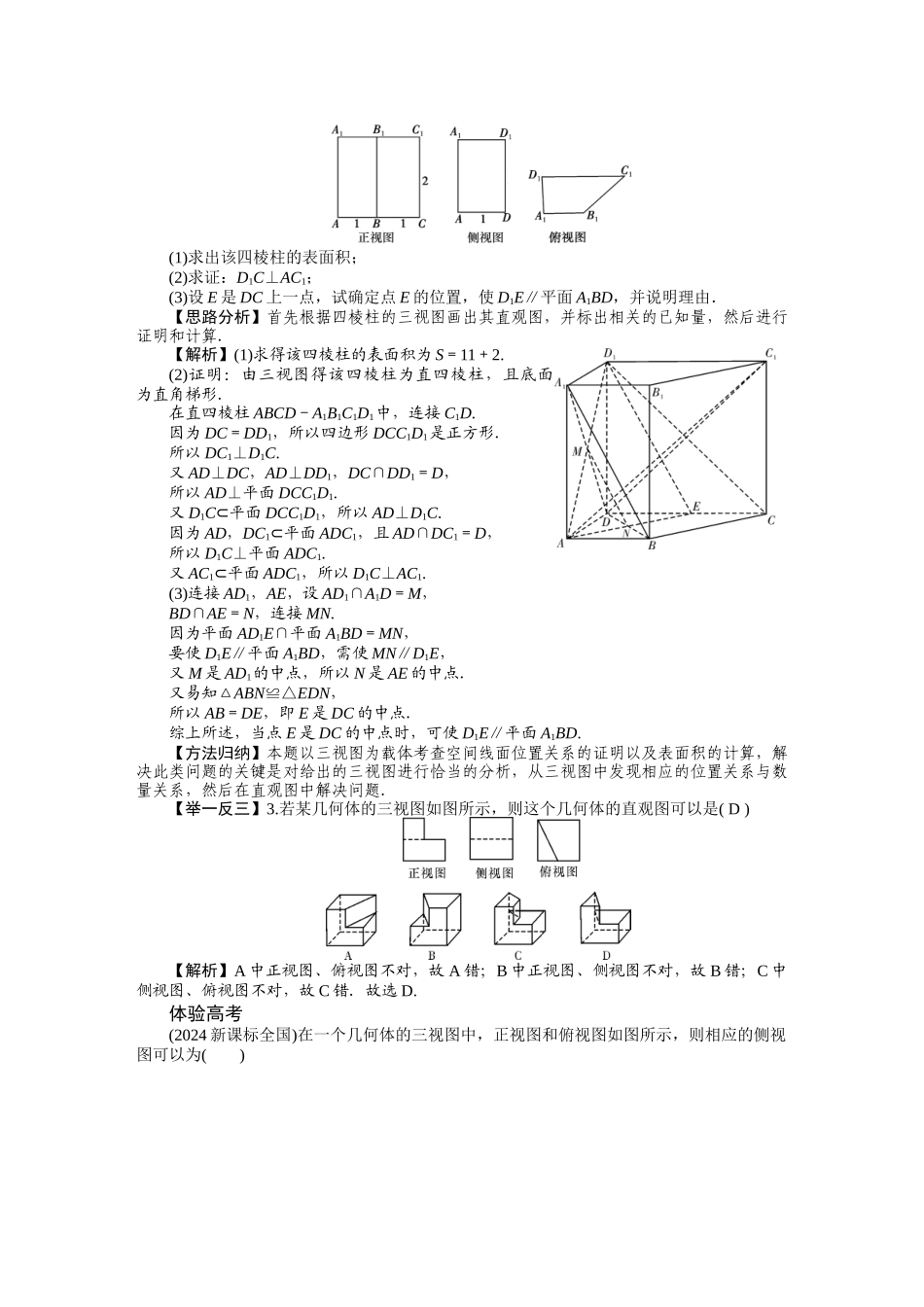
第十章 立体几何高考导航考纲要求备考策略 1.认识柱、锥、台、球及其简单组合体的结构特征,并能用这些特征描述现实生活中简单物体的结构. 2.能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别三视图表示的立体模型,会用斜二测画法画直观图. 3.会用平行投影与中心投影画出简单空间图形的三视图与直观图,了解空间图形的不同表现形式.会画某些建筑物的三视图与直观图. 4.了解球、棱柱、棱锥、台的表面积和体积的计算公式. 5.理解空间直线、平面之间的位置关系. 6.理解空间线线、线面、面面平行的判定和性质,理解空间线线、线面、面面垂直的判定和性质. 7.了解空间向量的概念和空间向量的基本定理及其意义,掌握空间向量的正交分解及其坐标表示. 8.掌握空间向量的线性运算及其坐标表示. 9.掌握空间向量的数量积及其坐标表示,能运用向量的数量积推断向量的共线与垂直. 10.理解直线的方向向量与平面的法向量. 11.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直、平行关系. 12.能用向量方法证明有关直线和平面位置关系的一些定理(包括三垂线定理). 13.能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题,了解向量方法在讨论立体几何问题中的应用. 立体几何是历年高考的重点,湖南省 2024 年高考对本章内容考查的是第 3、19 题,共 17 分,占总分的12%.一般以选择题或填空题的形式考查点、线、面之间的位置关系,三视图与空间几何体的结构特征等内容;解答题主要以空间几何体为载体,考查判定平行、垂直等位置关系或计算多面体的面积与体积、空间角等. 复习时采纳以下应对策略: 1.要有空间概念,可以通过实物模型对比直观图,提高空间想象能力. 2.夯实基础知识,立体几何的主要问题就是点、线、面之间的位置关系,空间中的三种角(线线所成角、线面所成角、二面角),另外三视图和直观图结合的题目也要引起重视. 3.狠抓法律规范解题,立体几何大题是高考的中档题目,步骤一般要求较严,要注意叙述正确,定理条件一定要清楚. 4.掌握图形构造和计算,立体几何的难题常常是小题,如构造图形进行推断的题目或图形比较复杂的计算题等.知识网络10.1 空间几何体的结构及其三视图和直观图考点诠释重点:掌握简单几何体和简单旋转体的有关概念和结构特征,掌握斜二测画法与三视图的画法及应用.难点:由三视图分析几何体的结构及性质...