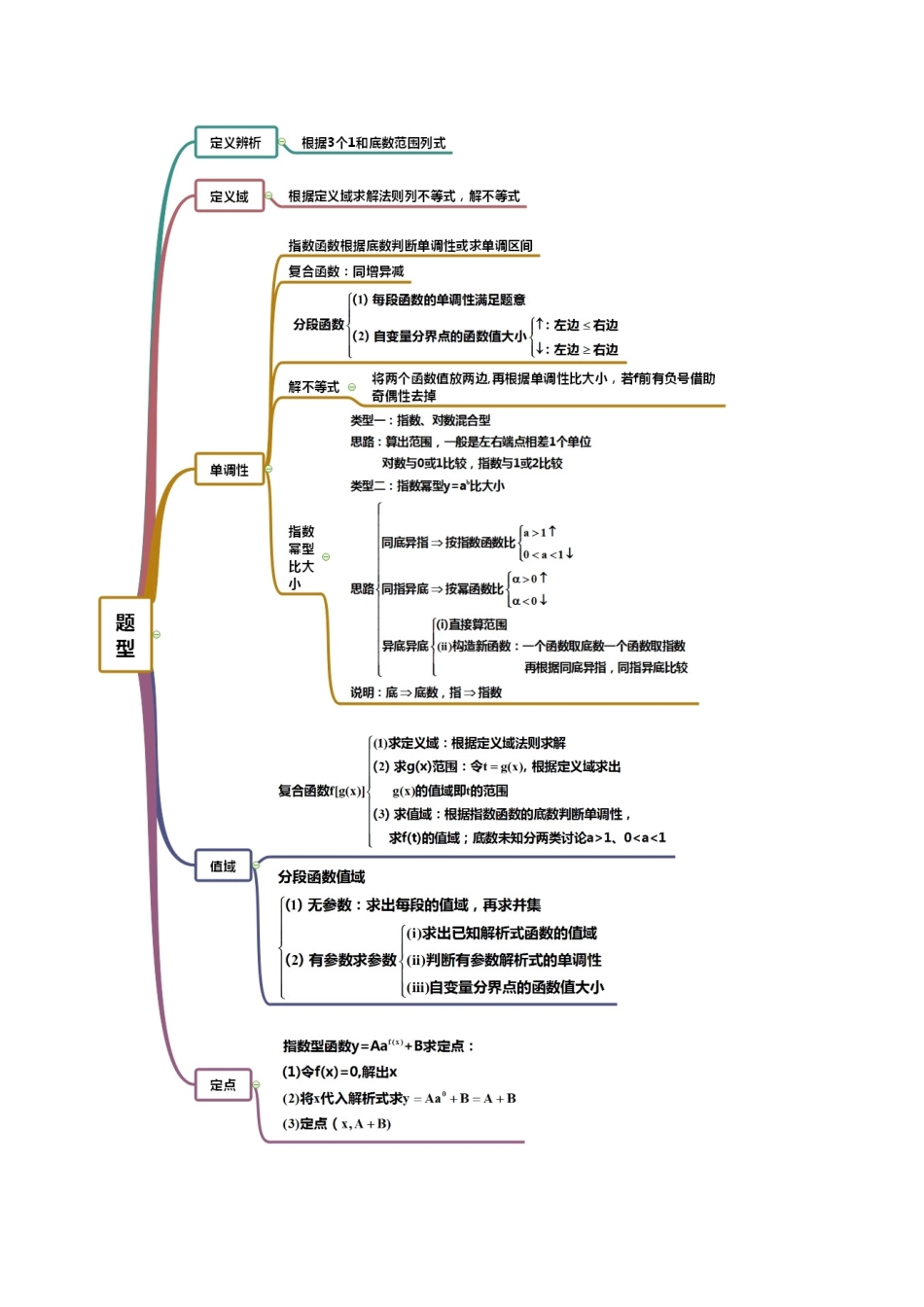
考点 9:指数函数【思维导图】【常见考法】考法一:定义辨析 1.下列函数:①;②;③;④(且).其中,指数函数的个数是 。【答案】1【解析】①函数是二次函数;②函数底数小于,故不是指数函数;③函数为,故不是指数函数;④且,可得出且,则是指数函数。指数函数个数为 1.2.若函数是自变量)是指数函数,则 a 的取值范围是 。【答案】且【解析】函数是自变量)是指数函数解得:且3.若函数是指数函数,则实数的值为_________.【答案】2【解析】因为函数是指数函数,所以且,解得.故答案为:2考法二:定义域1.函数 f(x)=的定义域为 。【答案】(−3,0]【解析】要使函数式有意义,需,则函数的定义域为(−3,0].2.函数的定义域为______________.【答案】【解析】换元,得出,解得(舍去)或,即,解得.因此,函数的定义域为,故答案为.3.设函数 f(x)=,则函数 f()的定义域为 。【答案】【解析】因为,所以,因为,所以的定义域为.4. 函数 y=的定义域是(-∞,0],则 a 的取值范围为 。【答案】(0,1)【解析】要使函数且有意义,则 ,即 ,当时,;当时,,因为的定义域为所以可得符合题意,的取值范围为.5.已知 f(x)=的定义域为 R,则实数 a 的取值范围是______.【答案】[-1,0]【解析】 f(x)的定义域为 R,∴0 对任意 x∈R 恒成立,即恒成立,即 x2+2ax﹣a≥0 对任意 x∈R 恒成立,∴△=4a2+4a≤0,则﹣1≤a≤0.故答案为[1﹣ ,0].考法三:单调性1.函数的单调递增区间为 。【答案】【解析】因为函数的单调递减区间为,所以原函数的单调递增区间为.2.函数的单调减区间为 。【答案】【解析】设,则由.得到,即函数的定义域.又.所以在上单调递减。3.已知函数,则不等式的解集为 。【答案】【解析】可知函数为减函数,由,可得,整理得,解得,所以不等式的解集为.4.若函数单调递增,则实数 a 的取值范围是 。【答案】【解析】函数单调递增,解得所以实数的取值范围是.5.a=212,b=313,c=515则a,b,c的大小关系为 。【答案】c
0,b>0,c>0,且:a6=23−8 ,b6=32=9,∴b>a;a10=25=32, c10=52=25,∴a>c,综上可得:c