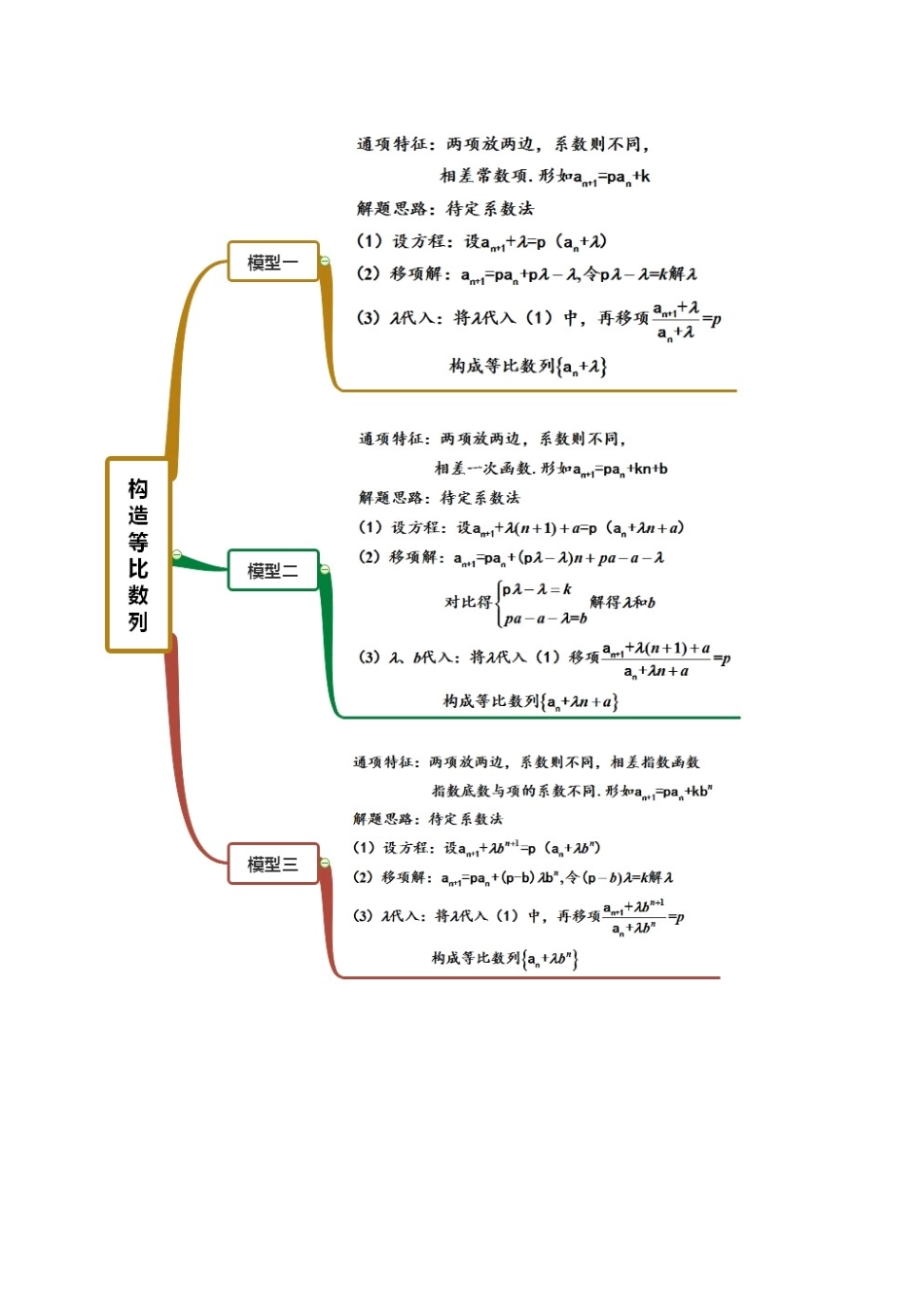
考点 20 递推公式求通项(第二课时)【思维导图】【常见考法】考法一:构造等差数列1.已知数列满足,则__________.【答案】【解析】由题, 则则数列是以为首项,2 为公差的等差数列,则即答案为.2.在数列中,,,则这个数列的通项= 。 【答案】【解析】 ,等式两边同时取倒数得:,则,∴,,,当 时, 亦成立,综上所述3.已知数列的前 n 项和为,,,则______.【答案】【解析】因为则可化简为等式两边同时除以可得,即所以数列为等差数列,首项,公差 所以即故答案为: 4.各项均正的数列满足,则等于 。【答案】【解析】两边同除以,得,则为首项为 2,公差为 1 的等差数列,∴则5.已知数列{an}满足 a1=1,an-an+1=nanan+1(n∈N*),则 an=________.【答案】【解析】由 an-an+1=nanan+1得=n,则由累加法得=1+2+…+(n-1)=,又因为 a1=1,所以,所以 an=.考法二:构造等比数列1.已知数列满足,且,则________________.【答案】【解析】由可得:,所以是以 1 为首项 3 为公比的等比数列,所以,故.2.已知数列满足,则数列的通项公式_________.【答案】【解析】设①将代入①式,得,等式两边消去,得,两边除以,得,则,代入①式得②由及②式得,则,则数列是以为首项,以为公比的等比数列,所以,所以.故答案为:.3.设为数列的前项和,,且,则_.【答案】.【解析】由两边同除以,整理得,令,则,∴,又由解得,∴ 。∴数列是首项为,公比为的等比数列。∴。∴,∴,4.已知数列满足, (),则__________.【答案】【解析】由 (),可得,于是,又,∴数列{﹣1}是以 2 为首项,为公比的等比数列,故﹣1=∴an=(n∈N*).故答案为.考法三:周期数列1.数列中,若,则 。【答案】【解析】,则,所以,所以数列是周期数列,周期为 2. 又, , ,,即.2.已知数列中,,,则的值是 。【答案】【解析】因为,,所以,,,,可知数列的取值有周期,周期为 3,所以,3.已知数列满足,,则 。【答案】【解析】依题意,,,所以,所以数列是周期为的数列,且每项的积为,故.4.已知数列中,,,且,则的值为 。【答案】2【解析】因为,由,,得;由,,得;由,,得;由,,得;由,,得;由,,得由此推理可得数列是一个周期为 6 的周期数列,所以。5.数列满足,(),则 。【答案】【解析】因为数列满足,(),所以所以是公比为 2 的等比数列,所以6.已知数列中,,则 。【答案】1...