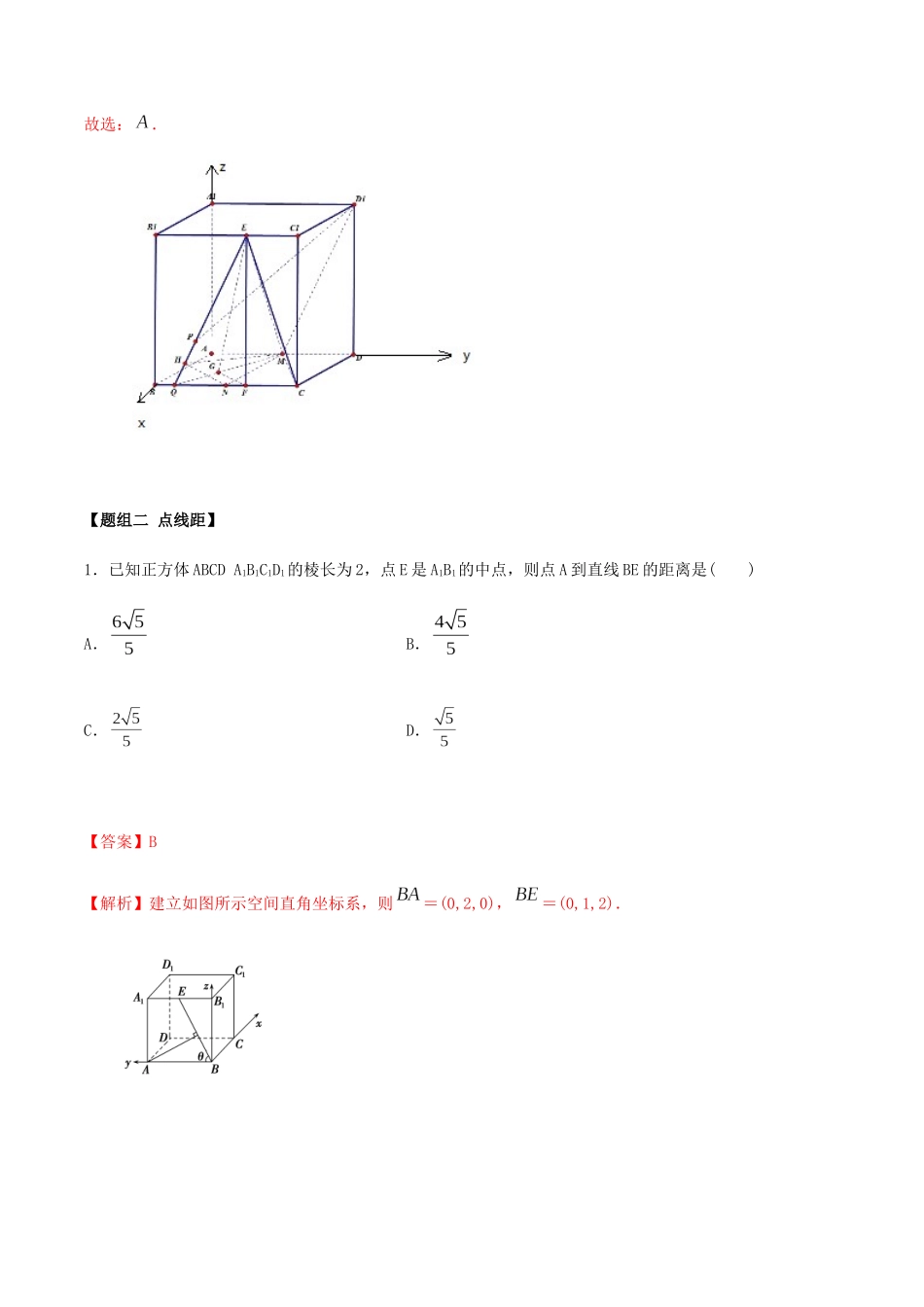
考点 27 空间向量求空间距离【题组一 两点距】1.已知点,,则的最小值为( ).A.B.C.D.【答案】C【解析】因为,所以当所以当时有最小值,故选:C.2.在空间直角坐标系中,设,若,则实数 a 的值是( )A.3 或 5B.或C.3 或D.或 5【答案】A【解析】由空间中两点的距离公式,可得,解得或.故选:A.3.设点 M 是棱长为 2 的正方体 ABCD-A1B1C1D1的棱 AD 的中点,点 P 在面 BCC1B1所在的平面内,若平面 D1PM分别与平面 ABCD 和平面 BCC1B1所成的锐二面角相等,则点 P 到点 C1的最短距离是( )A.B.C.1D.【答案】A【解析】如图,过点作的平行线交于点、交于点,连接,则是平面与平面的交线,是平面与平面的交线.与平行,交于点,过点作垂直于点,则有,与平面垂直,所以,与垂直,即角是平面与平面的夹角的平面角,且,与平行交于点,过点作垂直于点,同上有:,且有,又因为,故,而,故,而四边形一定是平行四边形,故它还是菱形,即点一定是的中点,点到点的最短距离是点到直线的距离,以为原点,为轴,为轴,为轴,建立空间直角坐标系,,, ,, ,点到点的最短距离:.故选:.【题组二 点线距】1.已知正方体 ABCD A1B1C1D1的棱长为 2,点 E 是 A1B1的中点,则点 A 到直线 BE 的距离是( )A.B.C.D.【答案】B【解析】建立如图所示空间直角坐标系,则=(0,2,0),=(0,1,2).∴cosθ==.∴sinθ=.故点 A 到直线 BE 的距离 d=||sinθ=2×.故答案为 B【题组三 点面距】1.如图,在直三棱柱中,,,为的中点.(1)求证:平面;(2)若,且,求到平面的距离.【答案】(1)证明见解析;(2).【解析】(1)证明:在直三棱柱中,,,为的中点.所以,因为,所以平面;(2)因为,,所以,由(1)可知,所以,即,可得,所以.以为原点建立如下图所示的空间直角坐标系:则,所以,设平面的法向量为,则,即,令,解得,由点到平面距离的向量求法可得.2.如图,在四棱锥中,底面为直角梯形,,,为的中点,,平面平面.(1)求证:平面平面;(2)记点到平面的距离为,点到平面的距离为,求的值.【答案】(1)详见解析;(2)【解析】(1)因为三角形为等边三角形,,所以.因为底面为直角梯形,,,为的的中点,,所以四边形是正方形,所以,因为,所以平面.因为,所以平面,由于平面,所以平面平面.(2)由(1)知两两垂直,建立如图所示的空间直角坐标系,不妨设,则,,,,.,.设平面的法向量为,...