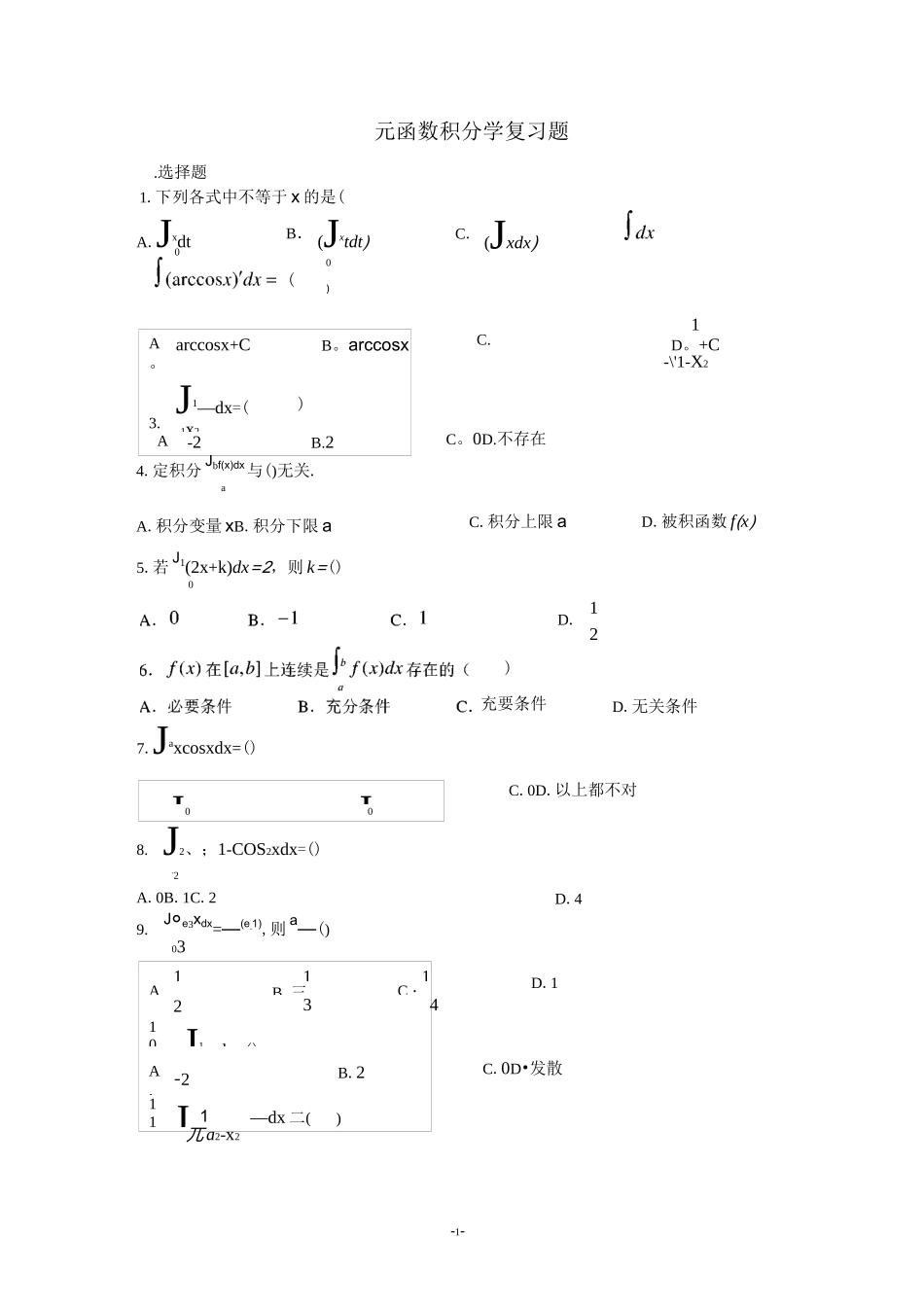
-1-.选择题1.下列各式中不等于 x 的是(A.JxdtB.元函数积分学复习题0(Jxtdt)0)C. (Jxdx)A。arccosx+CB。arccosx3. J1—dx=(_1x2)A.-2B.2(4.定积分 Jbf(x)dx与()无关.aC.1D。+C-\'1-X2C。0D.不存在A.积分变量 xB.积分下限 aC.积分上限 aD.被积函数 f(x)5.若 J1(2x+k)dx=2,则 k=()0D.)充要条件12D.无关条件A.JaxcosxdxB.2Jaxcosxdx007.Jaxcosxdx=()C.0D.以上都不对8. J2、;1-COS2xdx=()-2A.0B.1C.29.J°e3xdx=—(e-1),则 a—()03D.4111A —B.三C・23410 J1x3dx=()-1A.-2B.211 J.1—dx 二()兀 a2-x2D.1C.0D•发散-2-C.必存在唯一点 g,使 f(g)=°D.不一定存在 g,使 f(g)=°15o 设 F(x)=Jx+2Kesintsintdt,贝yF(x)为().xA.正常数 Bo 负常数 C.恒为零 Do 不为常数16o 设 f(x)在[a,b]上满足积分中值定理的条件,且 Jbf(x)dx=f(g)(b—a),其中a()oAog是b,订上任一点 Bog是[a,b]上必存在的某一点Cog是[a,b]上唯一的某一点 Dog是[a,b]的中点—(x2+1),°A.1B。213.f(x)=Jsinxsin(12,0A.高阶无穷小C。3D.4g(x)=x3+x4,则当 xT°时,f(x)是 g(x)的(B。同阶但非等阶无穷小).C.14等阶无穷小 D.低阶无穷小设Jbf(x)dx=°,且 f(x)在[a,b]上连续,则在[a,b]上().Aof(x)三°Bo 必存在点 g,使 fG)=°A. J;f(t)dt>J;g(t)dt22CoJ1f(t)dt>J1g(t)dtBoJ;f(t)dt°,广(x)<°,f"(x)>°,令19o)o23.4.-3-S=Jbf(x)dx,S1a=f(b)(b-a),S2[f(a)+f(b)](b-°),则().A.S