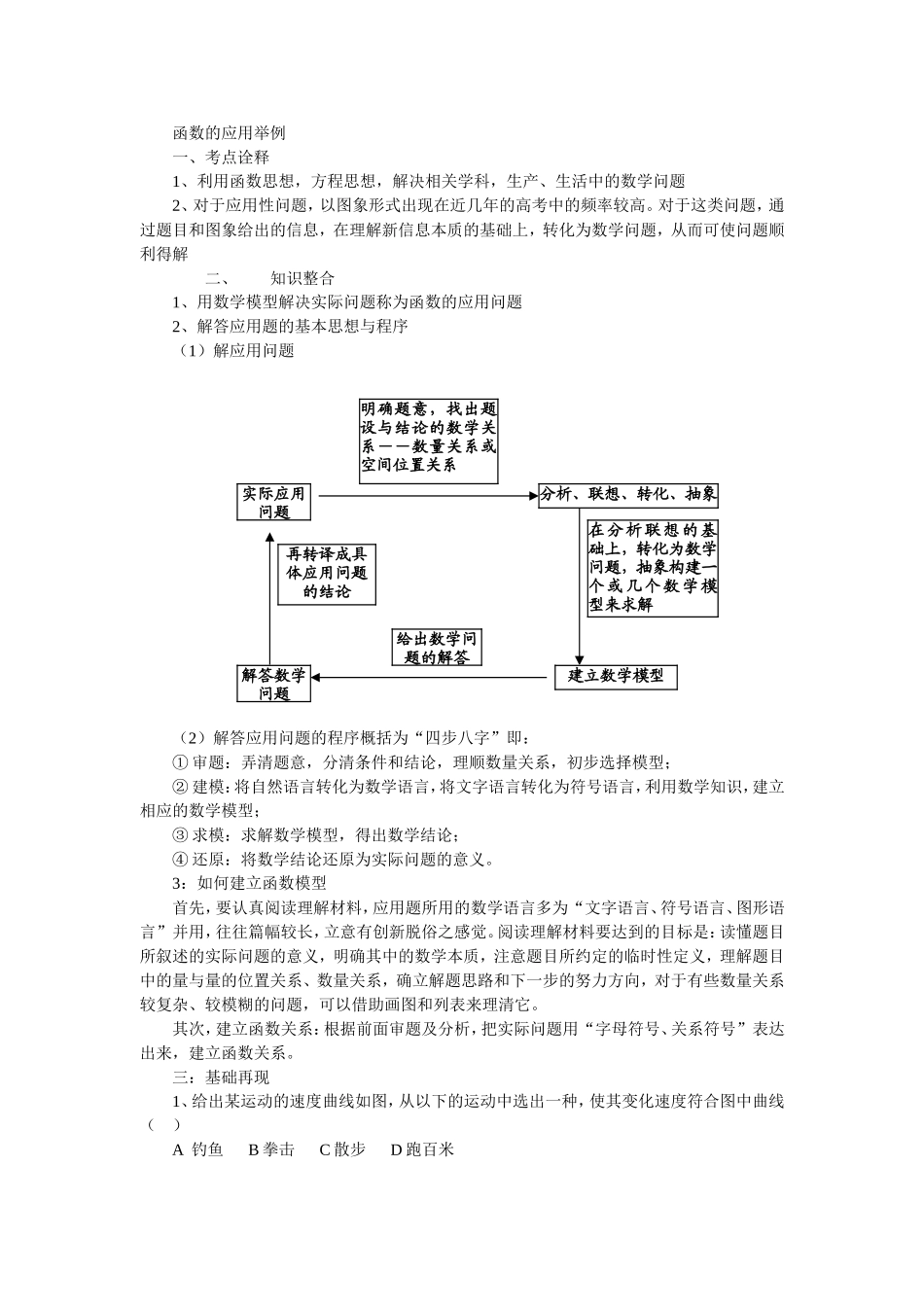
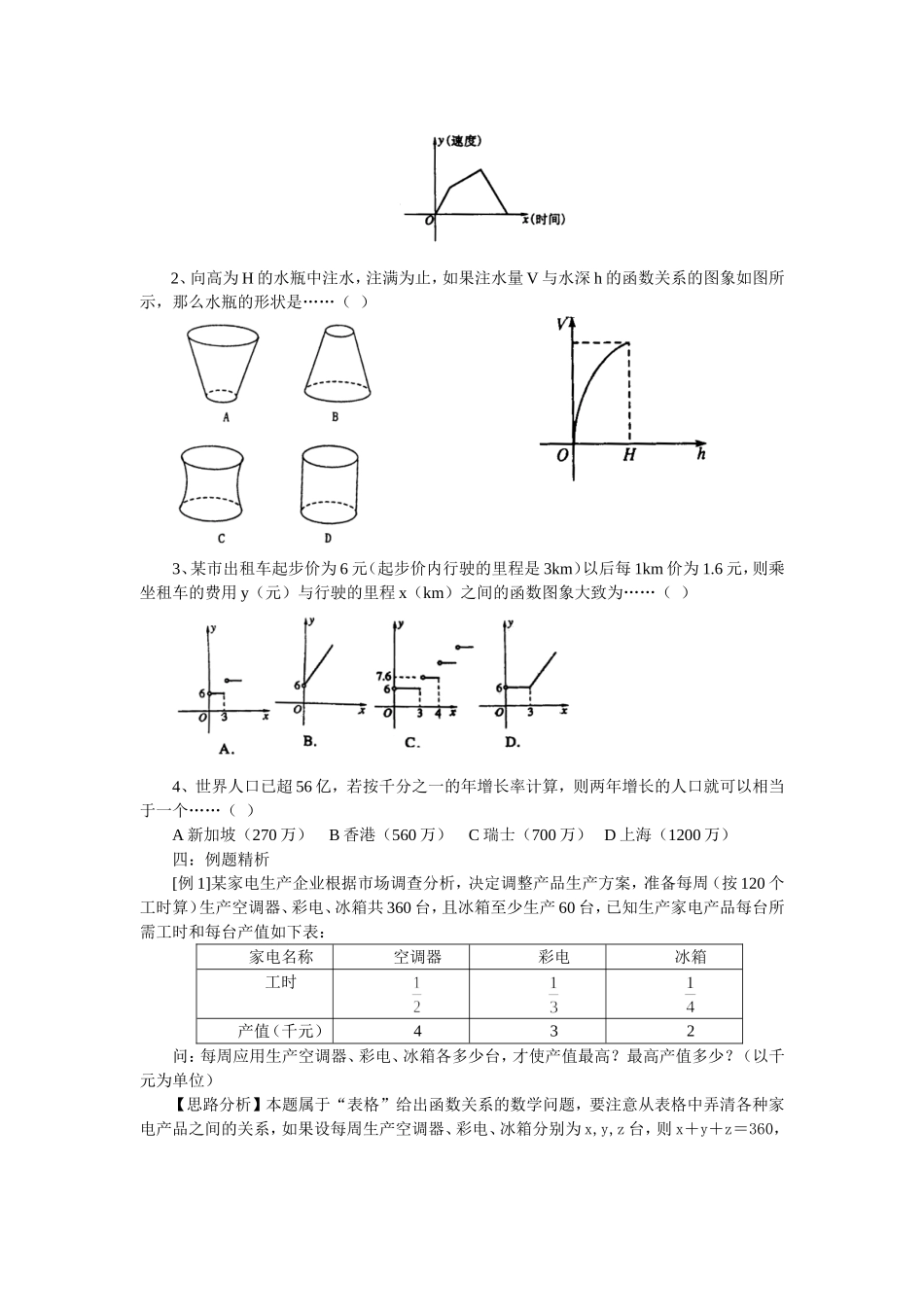
函数的应用举例一、考点诠释1、利用函数思想,方程思想,解决相关学科,生产、生活中的数学问题2、对于应用性问题,以图象形式出现在近几年的高考中的频率较高。对于这类问题,通过题目和图象给出的信息,在理解新信息本质的基础上,转化为数学问题,从而可使问题顺利得解二、知识整合1、用数学模型解决实际问题称为函数的应用问题2、解答应用题的基本思想与程序(1)解应用问题(2)解答应用问题的程序概括为“四步八字”即:① 审题:弄清题意,分清条件和结论,理顺数量关系,初步选择模型;② 建模:将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识,建立相应的数学模型; ③ 求模:求解数学模型,得出数学结论; ④ 还原:将数学结论还原为实际问题的意义。3:如何建立函数模型首先,要认真阅读理解材料,应用题所用的数学语言多为“文字语言、符号语言、图形语言”并用,往往篇幅较长,立意有创新脱俗之感觉。阅读理解材料要达到的目标是:读懂题目所叙述的实际问题的意义,明确其中的数学本质,注意题目所约定的临时性定义,理解题目中的量与量的位置关系、数量关系,确立解题思路和下一步的努力方向,对于有些数量关系较复杂、较模糊的问题,可以借助画图和列表来理清它。其次,建立函数关系:根据前面审题及分析,把实际问题用“字母符号、关系符号”表达出来,建立函数关系。三:基础再现1、给出某运动的速度曲线如图,从以下的运动中选出一种,使其变化速度符合图中曲线 ( )A 钓鱼 B 拳击 C 散步 D 跑百米 明确题意,找出题设与结论的数学关系――数量关系或空间位置关系实际应用问题分析、联想、转化、抽象再转译成具体应用问题的结论在 分 析 联 想 的 基础上,转化为数学问题,抽象构建一个 或 几 个 数 学 模型来求解解答数学问题给出数学问题的解答建立数学模型2、向高为 H 的水瓶中注水,注满为止,如果注水量 V 与水深 h 的函数关系的图象如图所示,那么水瓶的形状是……( ) 3、某市出租车起步价为 6 元(起步价内行驶的里程是 3km)以后每 1km 价为 1.6 元,则乘坐租车的费用 y(元)与行驶的里程 x(km)之间的函数图象大致为……( )4、世界人口已超 56 亿,若按千分之一的年增长率计算,则两年增长的人口就可以相当于一个……( )A 新加坡(270 万) B 香港(560 万) C 瑞士(700 万) D 上海(1200 万)四:例题精析[例 1]某家电...