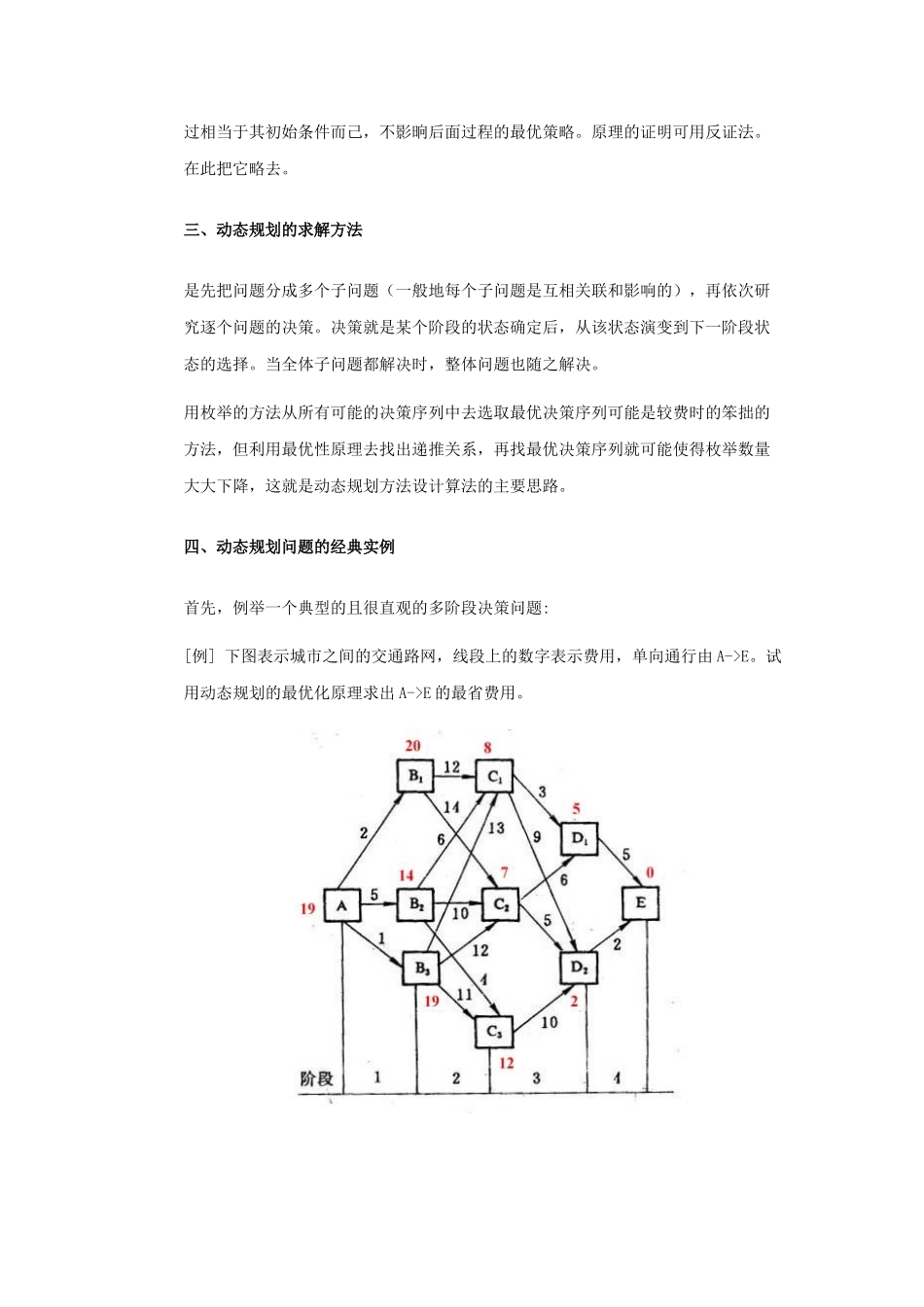
全国青少年信息学奥林匹克联赛动态规划算法一、动态规划的定义在现实生活中,有一类活动的过程,由于它的特殊性,可将过程分成若干个互相联系的阶段,在它的每一阶段都需要作出决策,从而使整个过程达到最好的活动效果。因此各个阶段决策的选取不能任意确定,它依赖于当前面临的状态,又影响以后的发展。当各个阶段决策确定后,就组成一个决策序列,因而也就确定了整个过程的一条活动路线。这种把一 个问题看作是一个前后关联具有链状结构的多阶段过程(如图)就称为多阶段决策过程,这种问题称为多阶段决策问题。在多阶段决策问题中,各个阶段采取的决策,一般来说是与时间有关的,决策依赖于当前状态,又随即引起状态的转移,一个决策序列就是在变化的状态中产生出来的,故有"动态"的含义,我们称这种解决多阶段决策最优化的过程为动态规划方法。应指出,动态规划是考察求解多阶段决策问题的一种途径、一种方法,而不是一种特殊算法。不像线性规划那样,具有一个标准的数学表达式和明确定义的一组规划。因此我们在学习时,除了要对基本概念和方法正确理解外,必须具体问题具体分析处理,以丰富的想象力去建立模型,用创造性的技巧去求解。二、动态规划最优化原理作为整个过程的最优策略具有这样的性质:即无论过去的状态和决策如何,对以前的决策所形成的状态而言,余下的诸决策必须构成最优策略。(无论过程的初始状态/初始决策是什么,其余决策活动必须相对于初始决策所产生的状态构成一个最优决策序列,才可能使整个决策活动构成最优决策序列。)简单地说,一个整体过程的最优策略的子策略一定是最优策略。利用这个原理,可以把多阶段决策问题的求解过程看成是一个连续的逆推过程。由后向前逐步推算。在求解时,各种状态前面的状态和决策,对后面的子问题,只不过相当于其初始条件而己,不影晌后面过程的最优策略。原理的证明可用反证法。在此把它略去。三、动态规划的求解方法是先把问题分成多个子问题(一般地每个子问题是互相关联和影响的),再依次研究逐个问题的决策。决策就是某个阶段的状态确定后,从该状态演变到下一阶段状态的选择。当全体子问题都解决时,整体问题也随之解决。用枚举的方法从所有可能的决策序列中去选取最优决策序列可能是较费时的笨拙的方法,但利用最优性原理去找出递推关系,再找最优决策序列就可能使得枚举数量大大下降,这就是动态规划方法设计算法的主要思路。四、动态规划问题的经典实例首先,例举一个典型的...