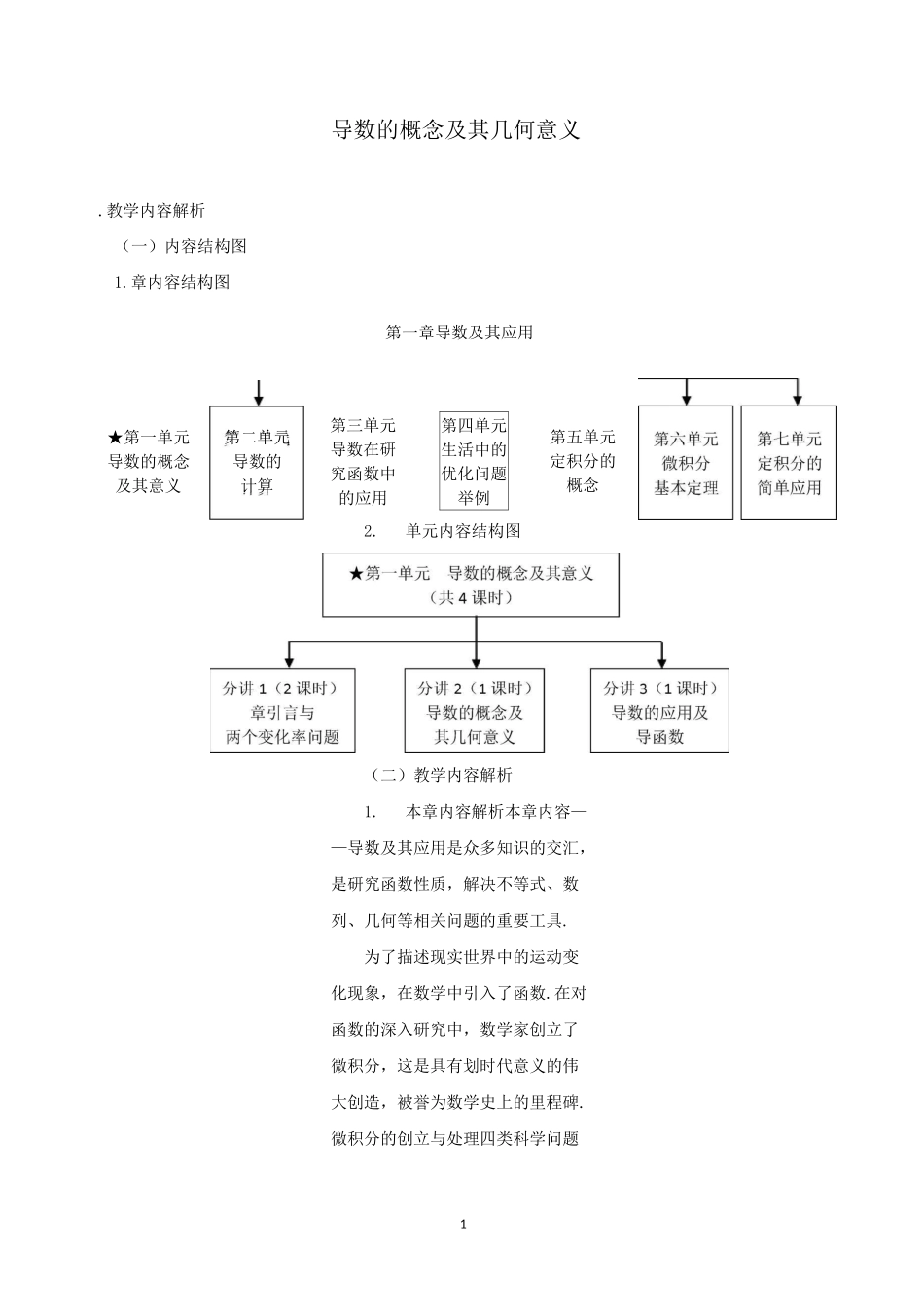
1导数的概念及其几何意义2.单元内容结构图(二)教学内容解析1.本章内容解析本章内容——导数及其应用是众多知识的交汇,是研究函数性质,解决不等式、数列、几何等相关问题的重要工具.为了描述现实世界中的运动变化现象,在数学中引入了函数.在对函数的深入研究中,数学家创立了微积分,这是具有划时代意义的伟大创造,被誉为数学史上的里程碑.微积分的创立与处理四类科学问题.教学内容解析(一)内容结构图1.章内容结构图第一章导数及其应用★第一单元导数的概念及其意义第三单元导数在研究函数中的应用第二单元导数的计算第四单元生活中的优化问题举例第五单元定积分的概念2直接相关:一是已知物体运动的路程作为时间的函数,求物体在任意时刻的速度与加速度,反之,已知物体的加速度作为时间的函数,求速度与路程;二是求曲线的切线;三是求函数的最大值与最小值;四是求长度、面积、体积和重心等.导数是微积分的核心内容之一,是现代数学的基本概念,蕴含着微积分的基本思想;它定量地刻画了函数的局部变化,是研究函数增减、变化快慢、最大(小)值等性质的基本方法.因而也是解决诸如增长率、膨胀率、效率、密度、加速度等实际问题的基本工具.2.本单元内容解析在本单元——导数的概念及其意义中,学生将通过实际情境,经历用平均变化率和瞬时变化率刻画实例的过程,感受数学的极限思想,抽象生成导数的概念,并通过函数图像直观感受导数的几何意义,感受“以直代曲”的极限思想.能够用导数的概念解释生活中的现象,体会用导数的知识研究函数的思想方法.通过具体实例感受导数在研究函数和解决实际问题中的作用,体会导数的意义.本单元设计了三个分讲,共计 43课时,分别是章引言与两个变化率问题(2 课时),导数的概念及其几何意义(1 课时),导数的应用及导函数(1 课时).3. 课时内容解析本课时内容选自人教社 A 版《选修 2-2》第一章导数及其应用中第一单元导数的概念及其意义中的单元分讲 2——导数的概念及其几何意义,用时 1 课时.本课时内容是在学生已经学习了分讲 1——章引言和两个变化率问题,即:已经研究了物理学中的平均速度和瞬时速度,几何学中的割线斜率和切线斜率的基础上,通过数学抽象,生成导数的概念及其表达.从“数”的角度理解导数概念的本质就是瞬时变化率•从“形”的角度,类比分讲 1 中曲线 f(X)二 x2在点(0,0)处的切线的斜率就是函数 f(x)二 x2在 x=0 处的导数的几何意义,抽象生成一般曲线 y ...