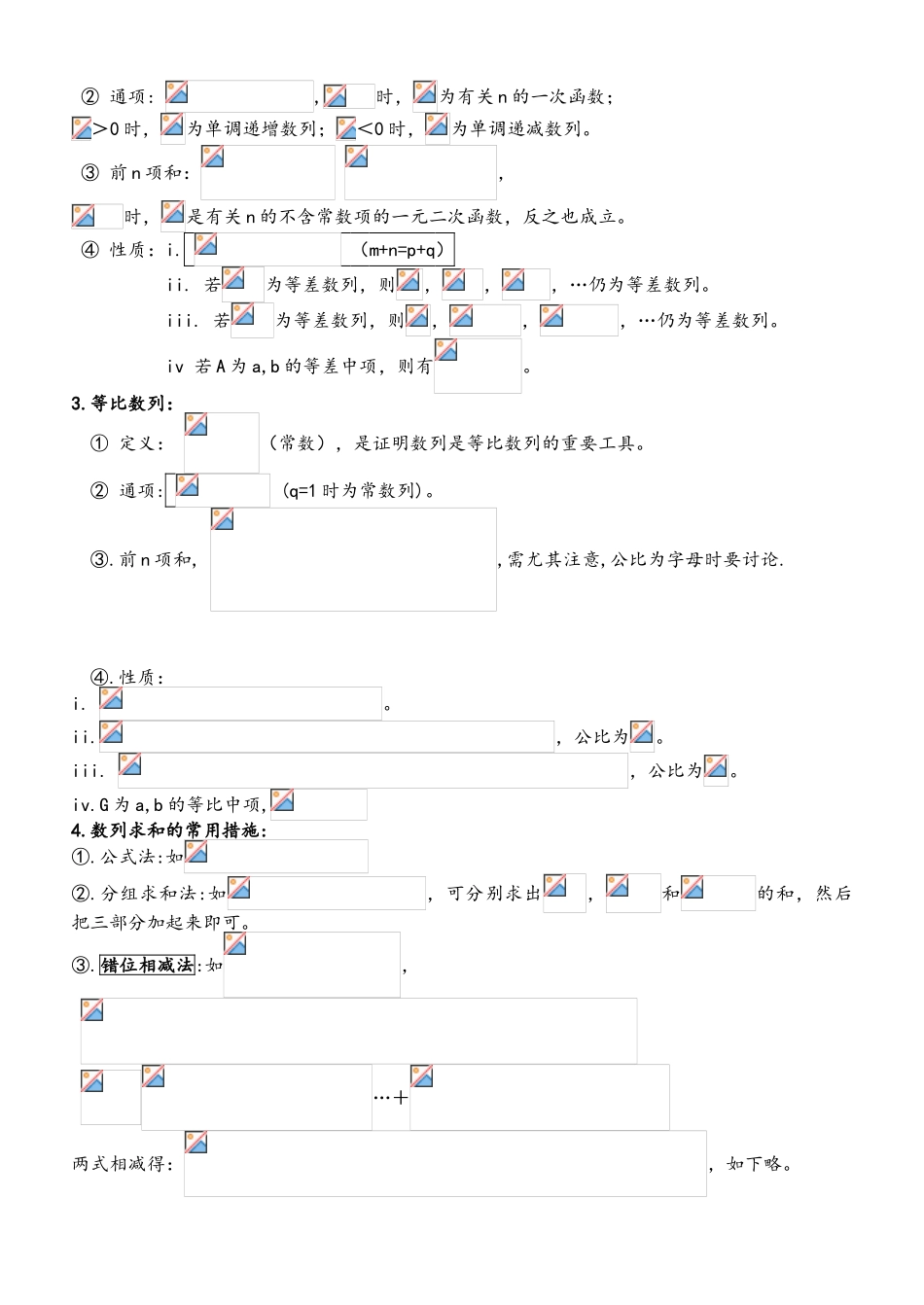
● 高二数学期中考知识点归纳资料第一章 解三角形1、三角形的性质:①.A+B+C=, , ②.在中, >c , <c ; A>B>, A>BcosA<cosB, a >b A>B ③.若为锐角,则>,B+C >,A+C >; >,>,+>2、正弦定理与余弦定理: ①.正弦定理: (2R 为外接圆的直径) 、、 (边化角)、 、 (角化边) 面积公式: ②.余弦定理:、、 、、 (角化边)3、常见的解题措施:(边化角或者角化边)第二章 数列1、数列的定义及数列的通项公式: ①. ,数列是定义域为 N 的函数,当 n 依次取 1,2,时的一列函数值 ②. 的求法:i.归纳法ii. 若,则不分段;若,则分段iii. 若,则可设解得 m,得等比数列iv. 若,先求,再构造方程组:得到有关和的递推关系式例 如 :先 求, 再 构 造 方 程 组 :( 下 减 上 )2.等差数列: ① 定义:=(常数),证明数列是等差数列的重要工具。 ② 通项: ,时,为有关 n 的一次函数;>0 时,为单调递增数列;<0 时,为单调递减数列。 ③ 前 n 项和: ,时,是有关 n 的不含常数项的一元二次函数,反之也成立。 ④ 性质:i. (m+n=p+q) ii. 若为等差数列,则,,,…仍为等差数列。 iii. 若为等差数列,则,,,…仍为等差数列。 iv 若 A 为 a,b 的等差中项,则有。3.等比数列: ① 定义: (常数),是证明数列是等比数列的重要工具。 ② 通项: (q=1 时为常数列)。③.前 n 项和, ,需尤其注意,公比为字母时要讨论.④.性质:i. 。ii.,公比为。iii. ,公比为。iv.G 为 a,b 的等比中项,4.数列求和的常用措施:①.公式法:如②.分组求和法:如,可分别求出,和的和,然后把三部分加起来即可。③.错位相减法:如, …+两式相减得:,如下略。 ④.裂项相消法:如, 等。⑤.倒序相加法.例:在 1 与 2 之间插入 n 个数,使这 n+2 个数成等差数列, 求:,(答案:)第三章 不等式1.不等式的性质:① 不等式的传递性:② 不等式的可加性:推论: ③ 不等式的可乘性:④ 不等式的可乘方性:2.一元二次不等式及其解法:①.重视三者之间的亲密联络。 如:>0 的解为:<x<, 则=0 的解为; 函数的图像开口向下,且与 x 轴交于点,。对于函数,一看开口方向,二看对称轴,从而确定其单调区间等。②.注意二次函数根的分布及其应用. 如:若方程的一种根在(0,1)上,另一种根在(4,5)上,则有>0 且<0 且<0 且>03.不等式...