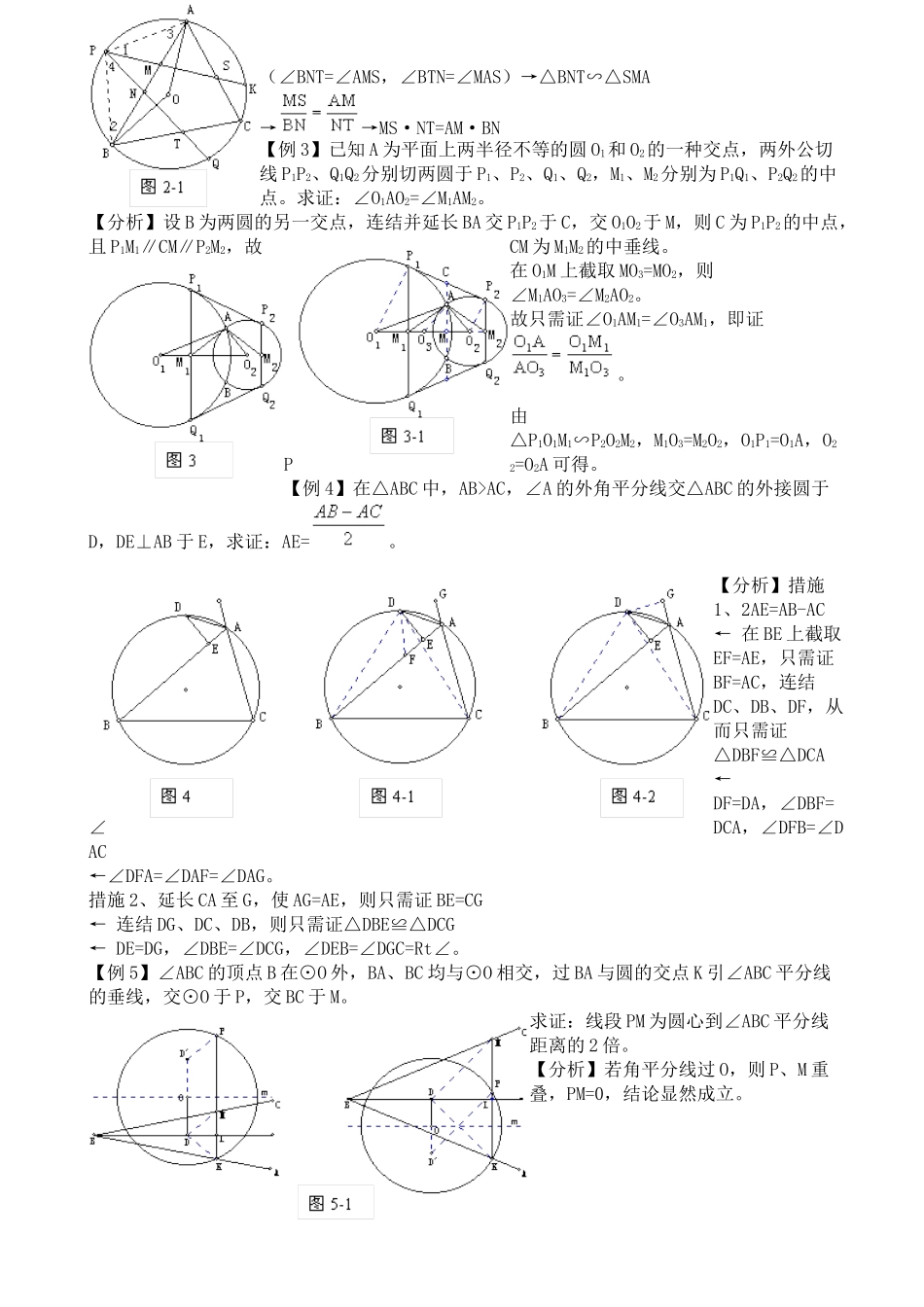
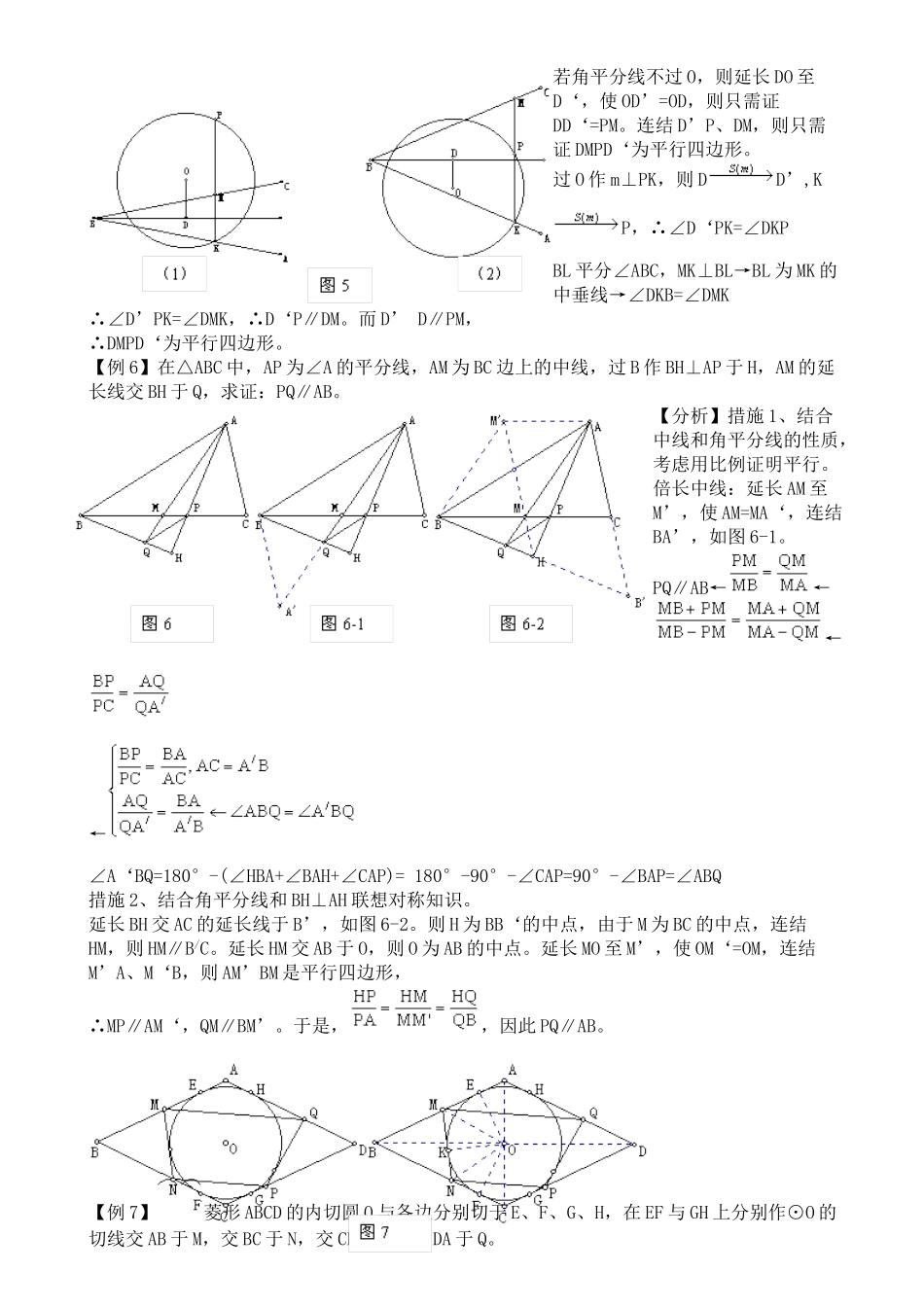
竞赛专题讲座 04-平面几何证明[竞赛知识点拨]1. 线段或角相等的证明(1)运用全等△或相似多边形;(2)运用等腰△;(3)运用平行四边形;(4)运用等量代换;(5)运用平行线的性质或运用比例关系(6)运用圆中的等量关系等。2. 线段或角的和差倍分的证明(1)转化为相等问题。如要证明 a=b±c,可以先作出线段 p=b±c,再去证明 a=p,即所谓“截长补短”,角的问题仿此进行。(2)直接用已知的定理。例如:中位线定理,Rt△斜边上的中线等于斜边的二分之一;△的外角等于不相邻的内角之和;圆周角等于同弧所对圆心角的二分之一等等。3. 两线平行与垂直的证明(1)运用两线平行与垂直的判定定理。(2)运用平行四边形的性质可证明平行;运用等腰△的“三线合一”可证明垂直。(3)运用比例关系可证明平行;运用勾股定理的逆定理可证明垂直等。【竞赛例题剖析】【例 1】从⊙O 外一点 P 向圆引两条切线 PA、PB 和割线 PCD。从 A 点作弦 AE 平行于 CD,连结BE 交 CD 于 F。求证:BE 平分 CD。【分析 1】构造两个全等△。连结 ED、AC、AF。CF=DF←△ACF≌△EDF←←←∠PAB=∠AEB=∠PFB【分析 2】运用圆中的等量关系。连结 OF、OP、OB。←∠PFB=∠POB←←注:连结 OP、OA、OF,证明 A、O、F、P 四点共圆亦可。【例 2】△ABC 内接于⊙O,P 是弧 AB 上的一点,过 P 作 OA、OB 的垂线,与 AC、BC 分别交于 S、T,AB 交于 M、N。求证:PM=MS 充要条件是 PN=NT。【分析】只需证, PM·PN=MS·NT。(∠1=∠2,∠3=∠4)→△APM∽△PBN→→PM·PN=AM·BN(∠BNT=∠AMS,∠BTN=∠MAS)→△BNT∽△SMA→→MS·NT=AM·BN【例 3】已知 A 为平面上两半径不等的圆 O1和 O2的一种交点,两外公切线 P1P2、Q1Q2分别切两圆于 P1、P2、Q1、Q2,M1、M2分别为 P1Q1、P2Q2的中点。求证:∠O1AO2=∠M1AM2。【分析】设 B 为两圆的另一交点,连结并延长 BA 交 P1P2于 C,交 O1O2于 M,则 C 为 P1P2的中点,且 P1M1∥CM∥P2M2,故CM 为 M1M2的中垂线。在 O1M 上截取 MO3=MO2,则∠M1AO3=∠M2AO2。故只需证∠O1AM1=∠O3AM1,即证。由△P1O1M1∽P2O2M2,M1O3=M2O2,O1P1=O1A,O2P2=O2A 可得。【例 4】在△ABC 中,AB>AC,∠A 的外角平分线交△ABC 的外接圆于D,DE⊥AB 于 E,求证:AE=。【分析】措施1、2AE=AB-AC ← 在 BE 上截取EF=AE,只需证BF=AC,连结DC、DB、DF,从而只需证△DBF...